Iz e-ELEKTROTEHNIKA plus
m (1 revision) |
|||
| Vrstica 13: | Vrstica 13: | ||
| - | Amplituda napetosti ima največjo vrednost pri frekvenci <latex>f_0</latex>, pri kateri je vsota susceptanc reaktivnih elementov enaka nič | + | Amplituda napetosti ima največjo vrednost pri frekvenci <latex>f_0</latex>, pri kateri je vsota susceptanc reaktivnih elementov enaka nič: |
| Vrstica 22: | Vrstica 22: | ||
| - | <latex>\underline Y (\omega _0 ) = G{\mathrm{ in } }\phi (\omega _0 ) = 0{\mathrm{ } } \Rightarrow {\mathrm{ } }U_{ {\mathrm{maks} }{\mathrm{.} } } = \left| {\underline U (\omega _0 )} \right| = I_{ {\mathrm{g m} } } /G | + | <latex>\underline Y (\omega _0 ) = G{\mathrm{ in } }\phi (\omega _0 ) = 0{\mathrm{ } } \Rightarrow {\mathrm{ } }U_{ {\mathrm{maks} }{\mathrm{.} } } = \left| {\underline U (\omega _0 )} \right| = I_{ {\mathrm{g m} } } /G.</latex> |
| - | + | Kazalce ostalih količin pa določajo takrat izrazi: | |
| Vrstica 34: | Vrstica 34: | ||
| - | Kazalec toka skozi upor je enak kazalcu toka vira; kazalca tokov v reaktivnih elementih sta si protifazna | + | Kazalec toka skozi upor je enak kazalcu toka vira; kazalca tokov v reaktivnih elementih sta si protifazna. Njuna vsota je enaka nič, vzporedno nihajno vezje se v resonanci vede kot upor. Med reaktivnima elementoma se neprenehoma izmenjuje energija. Poprečji ene in druge energije sta si enaki: |
| Vrstica 40: | Vrstica 40: | ||
| - | <latex>\overline W _{\mathrm{e} } (\omega _0 ) = {\textstyle{\frac{1}{4} } }C\left| {\underline U (\omega _0 )} \right|^2 = {\textstyle{\frac{1}{4} } }C\left( {\left| {\underline I _{\mathrm{g} } } \right|/G} \right)^2 | + | <latex>\overline W _{\mathrm{e} } (\omega _0 ) = {\textstyle{\frac{1}{4} } }C\left| {\underline U (\omega _0 )} \right|^2 = {\textstyle{\frac{1}{4} } }C\left( {\left| {\underline I _{\mathrm{g} } } \right|/G} \right)^2 .</latex> |
| - | + | Oba elementa skupaj pa imata vseskozi akumulirano energijo: | |
| Vrstica 49: | Vrstica 49: | ||
| - | Širino resonančne krivulje in kvaliteto določata enaka dogovora kot pred tem pri zaporednem nihajnem vezju. Bočni frekvenci tokovne resonančne krivulje izhajata iz enačb | + | Širino resonančne krivulje in kvaliteto določata enaka dogovora kot pred tem pri zaporednem nihajnem vezju. Bočni frekvenci tokovne resonančne krivulje izhajata iz enačb: |
| Vrstica 61: | Vrstica 61: | ||
| - | Od tu dalje je izpeljava povsem enaka tisti pri zaporednem nihajnem krogu; resonančna frekvenca je ponovno enaka geometrijski sredini bočnih frekvenc, pri kvaliteti pa se smiselno zamenjajo le podatki elementov nihajnega vezja | + | Od tu dalje je izpeljava povsem enaka tisti pri zaporednem nihajnem krogu; resonančna frekvenca je ponovno enaka geometrijski sredini bočnih frekvenc, pri kvaliteti pa se smiselno zamenjajo le podatki elementov nihajnega vezja: |
| Vrstica 71: | Vrstica 71: | ||
| - | '''Zgled 2 | + | '''Zgled 2''' |
| - | Vzporedni nihajni krog, <latex>R=10\,{\mathrm{k\Omega}}</latex>, <latex>L=50\,{\mathrm{\mu H}}</latex> in <latex>C=20\,{\mathrm{pF}}</latex>, vzbuja harmonični tokovni vir amplitude 12 mA in nastavljive frekvence. Izračunajmo resonančno frekvenco, kvaliteto, pasovno širino in energijo, ki se pri resonančni frekvenci »preliva« med reaktivnima elementoma | + | Vzporedni nihajni krog, <latex>R=10\,{\mathrm{k\Omega}}</latex>, <latex>L=50\,{\mathrm{\mu H}}</latex> in <latex>C=20\,{\mathrm{pF}}</latex>, vzbuja harmonični tokovni vir amplitude 12 mA in nastavljive frekvence. Izračunajmo resonančno frekvenco, kvaliteto, pasovno širino in energijo, ki se pri resonančni frekvenci »preliva« med reaktivnima elementoma. |
Redakcija: 22:25, 7. junij 2010
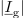
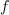
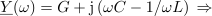
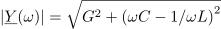
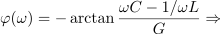
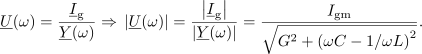
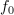
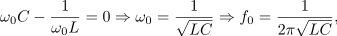
kar rezultira v enako enačbo kot pri zaporednem nihajnem krogu. Ko je vezje vzbujano s prav to frekvenco, je vzporedni nihajni krog v resonanci in v njem se zgodi napetostna resonanca. Admitanca, fazni kot in maksimalna vrednost amplitude napetosti so v resonanci sledeči:
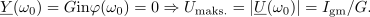
Kazalce ostalih količin pa določajo takrat izrazi:
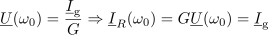
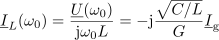
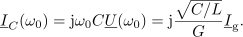
Kazalec toka skozi upor je enak kazalcu toka vira; kazalca tokov v reaktivnih elementih sta si protifazna. Njuna vsota je enaka nič, vzporedno nihajno vezje se v resonanci vede kot upor. Med reaktivnima elementoma se neprenehoma izmenjuje energija. Poprečji ene in druge energije sta si enaki:
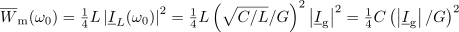
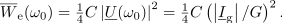
Oba elementa skupaj pa imata vseskozi akumulirano energijo:

Širino resonančne krivulje in kvaliteto določata enaka dogovora kot pred tem pri zaporednem nihajnem vezju. Bočni frekvenci tokovne resonančne krivulje izhajata iz enačb:
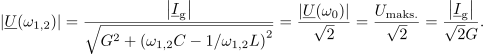
Amplituda napetosti doseže 70,7 % maksimalne vrednost pri frekvencah, pri katerih je absolutna vrednost vsote susceptanc kondenzatorja in tuljave enaka prevodnosti upora (slika 7):
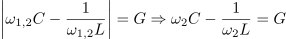
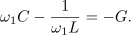
Od tu dalje je izpeljava povsem enaka tisti pri zaporednem nihajnem krogu; resonančna frekvenca je ponovno enaka geometrijski sredini bočnih frekvenc, pri kvaliteti pa se smiselno zamenjajo le podatki elementov nihajnega vezja:
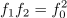
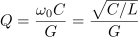
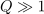
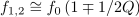
Zgled 2
Vzporedni nihajni krog,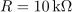
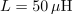
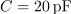
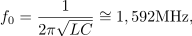
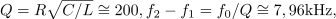
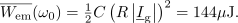
V resonanci je amplituda napetosti na vzporednih elementih 12 V, amplituda tokov v reaktivnih elementih pa je 2,4 A.
| | 6.4 Uporaba tokovne resonance |
