Iz e-ELEKTROTEHNIKA plus
m (1 revision) |
|||
| Vrstica 1: | Vrstica 1: | ||
| - | Integrirati (seštevati) začnemo od nekje in to počnemo do nekam. Začetek in konec sta stvar problema, ki ga luščimo, lahko pa se odločimo tudi drugače: da nas zanima integral funkcije ''f'' od izbranega »začetka« ''t''<sub>0</sub> do poljubnega »konca« ''t''<sup>*</sup> < ''t''<sub>1</sub>. V takšnem primeru je določen integral funkcije ''f'' oziroma vrednost ''G'' odvisna od ''t''<sup>*</sup> | + | Integrirati (seštevati) začnemo od nekje in to počnemo do nekam. Začetek in konec sta stvar problema, ki ga luščimo, lahko pa se odločimo tudi drugače: da nas zanima integral funkcije ''f'' od izbranega »začetka« ''t''<sub>0</sub> do poljubnega »konca« ''t''<sup>*</sup> < ''t''<sub>1</sub>. V takšnem primeru je določen integral funkcije ''f'' oziroma vrednost ''G'' odvisna od ''t''<sup>*</sup>, ''G'' je funkcija konca (''t''<sup>*</sup>) oziroma meje, do katere se vrši integriranje. Pisali bomo: |
<latex>{G({t^*}) \,=\, \int\limits_{t_0}^{t^*} {f(t){\rm{d}}t} .}</latex> | <latex>{G({t^*}) \,=\, \int\limits_{t_0}^{t^*} {f(t){\rm{d}}t} .}</latex> | ||
| - | Funcija ''G''(''t''<sup>*</sup>) je funkcija zgornje meje (''t''<sup>*</sup>) določenega integrala funkcije ''f''(''t''). | + | Funcija ''G''(''t''<sup>*</sup>) je funkcija zgornje meje (''t''<sup>*</sup>) določenega integrala funkcije ''f''(''t''). Poznavanje te funkcije je vsekakor koristno. V takem primeru integracija ni več potrebna, kajti za nek drug integracijski konec (''t''<sup>**</sup>) je dovolj, da zgornjo mejo ''t''<sup>**</sup> vstavimo v funkcijo ''G'', torej ''G''(''t''<sup>**</sup>), in že imamo odgovor. |
| - | Funkcija ''G'' ima tole očitno lastnost: ''G''(''t''<sub>0</sub>) = 0. Če konec integracije sovpada z začetkom, je že v neizlimitirani vsoti vsak sumand enak nič, torej tudi vsota. Glede na geometrijsko interpretacijo vrednosti določenega integrala moremo ''G''(''t''<sup>*</sup>) razumeti kot funkcijo ki pove, kako se spreminja oziroma »napreduje« vrednost površine«lika med absciso in funkcijo, ko se ''t''<sup>*</sup> pomika v desno. | + | Funkcija ''G'' ima tole očitno lastnost: ''G''(''t''<sub>0</sub>) = 0. Če konec integracije sovpada z začetkom, je že v neizlimitirani vsoti vsak sumand enak nič, torej tudi vsota. Glede na geometrijsko interpretacijo vrednosti določenega integrala moremo ''G''(''t''<sup>*</sup>) razumeti kot funkcijo, ki pove, kako se spreminja oziroma »napreduje« vrednost površine«lika med absciso in funkcijo, ko se ''t''<sup>*</sup> pomika v desno. |
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 09:27, 8. junij 2010
Integrirati (seštevati) začnemo od nekje in to počnemo do nekam. Začetek in konec sta stvar problema, ki ga luščimo, lahko pa se odločimo tudi drugače: da nas zanima integral funkcije f od izbranega »začetka« t0 do poljubnega »konca« t* < t1. V takšnem primeru je določen integral funkcije f oziroma vrednost G odvisna od t*, G je funkcija konca (t*) oziroma meje, do katere se vrši integriranje. Pisali bomo:
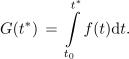
Funcija G(t*) je funkcija zgornje meje (t*) določenega integrala funkcije f(t). Poznavanje te funkcije je vsekakor koristno. V takem primeru integracija ni več potrebna, kajti za nek drug integracijski konec (t**) je dovolj, da zgornjo mejo t** vstavimo v funkcijo G, torej G(t**), in že imamo odgovor.
Funkcija G ima tole očitno lastnost: G(t0) = 0. Če konec integracije sovpada z začetkom, je že v neizlimitirani vsoti vsak sumand enak nič, torej tudi vsota. Glede na geometrijsko interpretacijo vrednosti določenega integrala moremo G(t*) razumeti kot funkcijo, ki pove, kako se spreminja oziroma »napreduje« vrednost površine«lika med absciso in funkcijo, ko se t* pomika v desno.
| | 5.4.2 Odvod funkcije zgornje meje določenega integrala |
