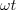Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (2 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | [[Image: | + | [[Image:eele_slika_visji_014.svg|thumb|Slika 14: Z naraščajočim časom kazalec <latex>{\underline w}</latex> enakomerno kroži s kotno hitrostjo <latex>\omega</latex>; njegova projekcija na realno os ustreza trenutni vrednosti napetosti <latex>u</latex>.]] |
| - | + | [[Image:eele_slika_visji_014.svg|thumb|Slika 15: Kazalec <latex>{\underline U}</latex> je mirujoč kazalec; določata ga amplituda in fazni kot napetosti <latex>u</latex>; kazalec <latex>{\underline w}</latex> je enakomerno vrteč kazalec; kot med njima je enak <latex>\omega t</latex>.]] | |
| - | [[Image: | + | |
Harmonično napetost <latex>u</latex> (ali tok <latex>i</latex>) poznamo; h kosinusni funkciji <latex>u</latex> »priložimo« še sinusno funkcijo <latex>v</latex>: | Harmonično napetost <latex>u</latex> (ali tok <latex>i</latex>) poznamo; h kosinusni funkciji <latex>u</latex> »priložimo« še sinusno funkcijo <latex>v</latex>: | ||
| Vrstica 14: | Vrstica 13: | ||
| - | V Gausovi ravnini bi ji ustrezal kazalec, ki oklepa z realno osjo kot <latex>\omega t + \alpha _u</latex> (slika | + | V Gausovi ravnini bi ji ustrezal kazalec, ki oklepa z realno osjo kot <latex>\omega t + \alpha _u</latex> (slika 14). Njegova absolutna vrednost je enaka amplitudi, argument pa je omenjen kot. In kaj se dogaja, ko čas »teče«, kot <latex>\omega t + \alpha _u</latex> pa narašča. Konica kazalca drsi po krožnici z radijem <latex>U_{\mathrm{m} }</latex>, iz česar sledi, da moremo harmonično napetost <latex>u</latex> predstaviti s projekcijo krožečega kazalca <latex>{\underline w}</latex> na realno ali (1) os. Iz adicijskih teoremov za sinusno in kosinusno funkcijo sledi:<ref><latex>\cos (p \pm q) = \cos p\cos q \mp \sin p\sin q{\mathrm{ in sin} }(p \pm q) = \sin p\cos q \pm \cos p\sin q</latex>.</ref> |
| Vrstica 32: | Vrstica 31: | ||
| - | »Uspelo« nam je oddvojiti harmonično časovno odvisnost od amplitude <latex>U_{\mathrm{m}}</latex> in faznega kota <latex>\alpha_{\mathrm{u}}</latex>. Tu je | + | »Uspelo« nam je oddvojiti harmonično časovno odvisnost od amplitude <latex>U_{\mathrm{m}}</latex> in faznega kota <latex>\alpha_{\mathrm{u}}</latex>. Tu je priložnost, da definiramo ''kazalec napetosti'' <latex>{\underline U}</latex>, in sicer na tale način: |
| Vrstica 38: | Vrstica 37: | ||
| - | Kazalec <latex>{\underline U}</latex> ima absolutno vrednost enako amplitudi <latex>U_{\mathrm{m}}</latex>, argument pa faznemu kotu <latex>\alpha_{\mathrm{u}}</latex> napetosti <latex>u</latex>; kazalec združuje oba vitalna podatka: amplitudo in fazni kot harmonične napetosti <latex>u</latex> (slika | + | Kazalec <latex>{\underline U}</latex> ima absolutno vrednost enako amplitudi <latex>U_{\mathrm{m}}</latex>, argument pa faznemu kotu <latex>\alpha_{\mathrm{u}}</latex> napetosti <latex>u</latex>; kazalec združuje oba vitalna podatka: amplitudo in fazni kot harmonične napetosti <latex>u</latex> (slika 15). Harmonična napetost <latex>u</latex> je sedaj: |
| Vrstica 44: | Vrstica 43: | ||
| - | Kar je v izpeljavi najbolj | + | Kar je v izpeljavi najbolj pomembno, napišimo še enkrat: |
| Vrstica 56: | Vrstica 55: | ||
| - | '''Zgled 2 | + | '''Zgled 2 ''' |
| - | Napetost <latex>u = 150\cos (300\,{{\rm{s}}^{{\rm{ - 1}}}} + 37^\circ )\,{\rm{V}}</latex>. Določimo kazalec napetosti! | + | Napetost <latex>u = 150\cos \,(300\,{{\rm{s}}^{{\rm{ - 1}}}} + 37^\circ )\,{\rm{V}}</latex>. Določimo kazalec napetosti! |
⇒ Dobimo sledeče: | ⇒ Dobimo sledeče: | ||
| Vrstica 66: | Vrstica 65: | ||
| - | '''Zgled 3 | + | '''Zgled 3 ''' |
| - | Kazalec <latex>\underline I = ( - 1\,\, - {\rm{j}})\,{\rm{A}}</latex> pripada harmoničnemu toku frekvence 100 Hz. Poiščimo <latex>i</latex> | + | Kazalec <latex>\underline I = ( - 1\,\, - {\rm{j}})\,{\rm{A}}</latex> pripada harmoničnemu toku frekvence 100 Hz. Poiščimo <latex>i</latex>. ⇒ Po izrazih sledijo: |
Trenutna redakcija s časom 16:41, 12. julij 2010
Harmonično napetost

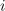


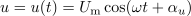
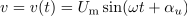


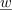
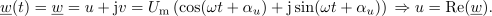
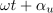
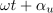
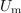

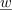
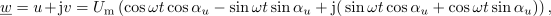
po ureditvi pa še:
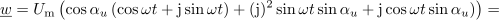
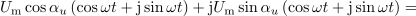
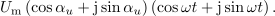
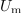
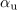
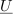
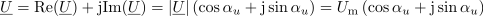
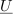
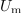
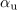



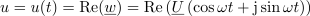
Kar je v izpeljavi najbolj pomembno, napišimo še enkrat:


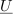
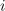
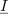
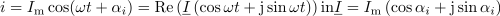
Zgled 2
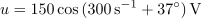
⇒ Dobimo sledeče:

Zgled 3
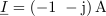

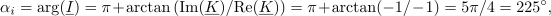
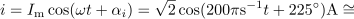
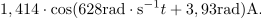
Glede na to, da grafično upodobitev kazalca opredeljujeta absolutna vrednost in kot, uporabljamo zanj tudi polarni zapis:

Opombe
- ↑ .
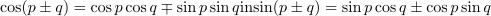
| | 1.3.3 Grafično seštevanje (odštevanje) kazalcev |