Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (One intermediate revision not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
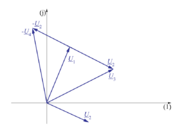
| - | [[Slika: | + | [[Slika:eele_slika_visji_016.svg|thumb|Slika 16: Vsoto in razliko kazalcev naredimo po trikotniškem oziroma paralelogramskem pravilu.]] |
| - | Kazalci kot »vektorji« izkažejo svojo prednost pri grafičnem upodabljanju; nastali sliki v kompleksni ravnini rečemo ''kazalčni diagram''. Kadar sta kazalca <latex>{\underline U _1}</latex> in <latex>{\underline U _2}</latex> podana kot kompleksni količini, ju seštejemo tako, da ločeno seštejemo njuna realna in ločeno njuna imaginarna dela, grafično pa ju seštejemo (kot pri vektorjih) po trikotniškem oziroma paralelogramskem pravilu. Kazalec <latex>{\underline U _3} = {\underline U _1} + {\underline U _2}</latex> pridobimo tako, da na konico enega kazalca priložimo drug kazalec, nato pa povežemo izhodišče s koncem slednjega (slika | + | Kazalci kot »vektorji« izkažejo svojo prednost pri grafičnem upodabljanju; nastali sliki v kompleksni ravnini rečemo ''kazalčni diagram''. Kadar sta kazalca <latex>{\underline U _1}</latex> in <latex>{\underline U _2}</latex> podana kot kompleksni količini, ju seštejemo tako, da ločeno seštejemo njuna realna in ločeno njuna imaginarna dela, grafično pa ju seštejemo (kot pri vektorjih) po trikotniškem oziroma paralelogramskem pravilu. Kazalec <latex>{\underline U _3} = {\underline U _1} + {\underline U _2}</latex> pridobimo tako, da na konico enega kazalca priložimo drug kazalec, nato pa povežemo izhodišče s koncem slednjega (slika 16). Podobno je pri odštevanju, <latex>{\underline U _4} = {\underline U _1} - {\underline U _2}</latex>, saj je <latex>{\underline U _4} = {\underline U _1} + (-{\underline U _2})</latex>; kazalec <latex>-{\underline U _2}</latex> je kazalcu <latex>{\underline U _2}</latex> nasproten oziroma ''protifazen''. |
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 16:42, 12. julij 2010
Kazalci kot »vektorji« izkažejo svojo prednost pri grafičnem upodabljanju; nastali sliki v kompleksni ravnini rečemo kazalčni diagram. Kadar sta kazalca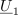
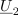
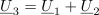
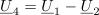
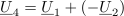
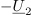
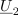
| | 1.3.4 »Prehitevanje in zaostajanje kazalcev« |