Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
| (5 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
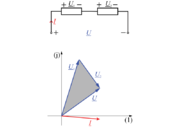
| - | [[Slika: | + | [[Slika:eele_slika_visji_068.svg|thumb|Slika 68: Impedančni delilnik in kazalčni diagram toka in napetosti ter napetostni trikotnik.]] |
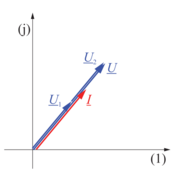
| - | [[Slika: | + | [[Slika:eele_slika_visji_076.svg|thumb|Slika 76: Delilnik oblikujeta upora, zato so vsi kazalci sofazni.]] |
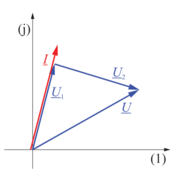
| - | [[Slika: | + | [[Slika:eele_slika_visji_075.svg|thumb|Slika 75: Delilnik oblikujeta upor in kondenzator; trikotnik napetosti je zato pravokoten.]] |
| - | Spomnimo se delilnikov napetosti v izvedbi z upori ali s kondenzatorji. Delitev napetosti na delne se je pri prvem izvedla v razmerju upornosti, pri drugem pa v razmerju recipročnih kapacitivnosti. Nekaj takega moremo pričakovati tudi od impedančnega delilnika v izmeničnem vezju; naj ga oblikuje zaporedno vezje dvopolov impedanc <latex>\underline Z _1</latex> in <latex>\underline Z _2</latex> (slika | + | Spomnimo se delilnikov napetosti v izvedbi z upori ali s kondenzatorji. Delitev napetosti na delne se je pri prvem izvedla v razmerju upornosti, pri drugem pa v razmerju recipročnih kapacitivnosti. Nekaj takega moremo pričakovati tudi od impedančnega delilnika v izmeničnem vezju; naj ga oblikuje zaporedno vezje dvopolov impedanc <latex>\underline Z _1</latex> in <latex>\underline Z _2</latex> (slika 68). Kazalci napetosti in delilno razmerje: |
| Vrstica 8: | Vrstica 8: | ||
| - | Delilno razmerje oziroma razmerje impedanc je tokrat kompleksno število | + | Delilno razmerje oziroma razmerje impedanc je tokrat kompleksno število. Ker pa sta impedanci poljubni, lahko to število leži kjerkoli v kompleksni ravnini, kar preprečuje, da bi možnosti delilnika takoj prepoznali. V pomoč nam bo kazalčni diagram, v katerem pritegne ''napetostni trikotnik'', ki delilno razmerje pokaže na grafični način. Odprtih je veliko možnosti in več trikotnikov: da kazalec <latex>\underline U _1</latex> prehiteva ali zaostaja za kazalcem <latex>\underline U _2</latex> in da sta v splošnem različnih absolutnih vrednosti. K razumevanju pripomore svoje tudi ''trikotniška neenačba'': absolutna vrednost enega kazalca je vedno manjša ali kvečjemu enaka vsoti absolutnih vrednosti drugih dveh. |
| - | '''Zgled 1 | + | '''Zgled 1''' |
| - | Na voljo imamo harmonično napetost frekvence 50 Hz in efektivne vrednosti 400 V ter žarnico (na nitko), ki ima pri napajanju z napetostjo efektivne vrednosti 230 V moč 100 W. Kako z uporabo impedančnega delilnika zagotoviti žarnici potrebno napetost? ⇒ Ker je žarnica uporovno breme, se ponuja uporovni delilnik. Delni napetosti sta takrat v fazi in v fazi s tokom (slika | + | Na voljo imamo harmonično napetost frekvence 50 Hz in efektivne vrednosti 400 V ter žarnico (na nitko), ki ima pri napajanju z napetostjo efektivne vrednosti 230 V moč 100 W. Kako z uporabo impedančnega delilnika zagotoviti žarnici potrebno napetost? ⇒ Ker je žarnica uporovno breme, se ponuja uporovni delilnik. Delni napetosti sta takrat v fazi in v fazi s tokom (slika 76). Napetostni trikotnik je sploščen, zato je efektivna vrednost napetosti na preduporu pač 170 V. Upornost predupora mora biti tolikšna, da bo pri efektivni vrednosti toka žarnice 100 W / 230 V = 435 mA efektivna vrednost napetosti na njem 170 V. Upornost predupora mora biti 391 <latex>\Omega</latex>. Nerodnost delilnika je ta, da vnaša izgubo energije. Predupor bi se namreč grel z močjo 74 W in izkoristek delilnika bi bil le 57,5 %. |
| - | Vsekakor bi bilo bolje, če bi predupor zamenjali s kondenzatorjem | + | Vsekakor bi bilo bolje, če bi predupor zamenjali s kondenzatorjem. Le-ta bi vnesel le jalovo energijo, izkoristka pa ne bi pokvaril. Kazalec napetosti žarnice je sofazen s kazalcem toka, kazalec napetosti na kondenzatorju pa za njim zaostaja (slika 75). Hipotenuza trikotnika pripada kazalcu napajalne napetosti. Iz Pitagorovega izreka sledi efektivna vrednost napetosti na kondenzatorju in znaša 327 V. Susceptanca (<latex>\omega C</latex>) potrebnega kondenzatorja mora biti enaka kvocientu efektivne vrednosti toka delilnika (435 mA) in efektivne vrednosti napetosti na kondenzatorju, kar znese 1,33 mS. Če slednje delimo z <latex>\omega=2 \pi f(\cong314\,{\mathrm{s}}^{-1})</latex>, dobimo kapacitivnost <latex>4,24\,{\mathrm{\mu F}}</latex>. |
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 12:25, 13. julij 2010
Spomnimo se delilnikov napetosti v izvedbi z upori ali s kondenzatorji. Delitev napetosti na delne se je pri prvem izvedla v razmerju upornosti, pri drugem pa v razmerju recipročnih kapacitivnosti. Nekaj takega moremo pričakovati tudi od impedančnega delilnika v izmeničnem vezju; naj ga oblikuje zaporedno vezje dvopolov impedanc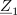
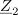
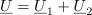
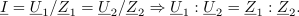
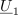
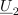
Zgled 1
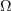
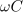
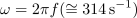
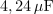
| | 3.2 Merjenje impedance |