Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (One intermediate revision not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | Če smo našli funkcijo ''F'', katere odvod je ''f'', je z njo določena funkcija ''G'' | + | Če smo našli funkcijo ''F'', katere odvod je ''f'', je z njo določena funkcija ''G''. Določena je vrednost ''G''(''t''<sub>1</sub>) in tudi vrednost določenega integrala ''I'', s katerim smo integriranje začeli: |
<latex>G(t)\, = \,F(t)\, -\, F({t_0}){\rm{ }}\,\,\,\,\, \Rightarrow \,\,\,\,\,{\rm{ }}G({t_1})\, = \,F({t_1})\, -\, F({t_0})\, =\, \int\limits_{t_0}^{t_1} {f(t){\rm{d}}t} \, =\, I.</latex> | <latex>G(t)\, = \,F(t)\, -\, F({t_0}){\rm{ }}\,\,\,\,\, \Rightarrow \,\,\,\,\,{\rm{ }}G({t_1})\, = \,F({t_1})\, -\, F({t_0})\, =\, \int\limits_{t_0}^{t_1} {f(t){\rm{d}}t} \, =\, I.</latex> | ||
Trenutna redakcija s časom 09:30, 8. junij 2010
Če smo našli funkcijo F, katere odvod je f, je z njo določena funkcija G. Določena je vrednost G(t1) in tudi vrednost določenega integrala I, s katerim smo integriranje začeli:
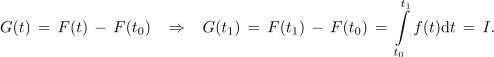
Od funkcije G, ki nam je veliko pomagala, se sedaj »poslovimo« in sklenimo:
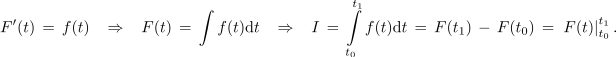
Določen integral I funkcije f na intervalu [t0, t1] izračunamo tako, da najdemo funkciji f njen nedoločen integral F, zatem pa tvorimo še razliko funkcijskih vrednosti funkcije F na zgornji in na spodnji integracijski meji.
 5.5 Nedoločen integral funkcije
| 5.7 Odvodi in integrali nekaterih elementarnih funkcij
|
