Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
| Vrstica 1: | Vrstica 1: | ||
Ali znamo reči kaj o odvodu funkcije ''G'' v točki ''t''<sup>*</sup> oziroma o limiti naslednjega kvocienta: | Ali znamo reči kaj o odvodu funkcije ''G'' v točki ''t''<sup>*</sup> oziroma o limiti naslednjega kvocienta: | ||
| + | |||
<latex>G^\prime \, = \,\mathop {\lim }\limits_{\Delta t \to 0} \frac{\Delta G}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{G({t^*} + \Delta t) - G(t)}{\Delta t}\, =\, ?</latex> | <latex>G^\prime \, = \,\mathop {\lim }\limits_{\Delta t \to 0} \frac{\Delta G}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{G({t^*} + \Delta t) - G(t)}{\Delta t}\, =\, ?</latex> | ||
| + | |||
Iz lastnosti integrala izhaja, da je števec v resnici določen integral funkcije ''f'' od ''t''<sup>*</sup> do ''t''<sup>*</sup> + Δ''t'', saj je | Iz lastnosti integrala izhaja, da je števec v resnici določen integral funkcije ''f'' od ''t''<sup>*</sup> do ''t''<sup>*</sup> + Δ''t'', saj je | ||
| + | |||
<latex>G({t^*} \,+\, \Delta t)\, - \,G({t^*}) \,=\, \int\limits_{t_0}^{{t^*} \,+\, \Delta t} {f(t){\rm{d}}t} \, -\, \int\limits_{t_0}^{t^*} {f(t){\rm{d}}t} \, =\, \int\limits_{t^*}^{{t^*}\, +\, \Delta t} {f(t){\rm{d}}t} ,</latex> | <latex>G({t^*} \,+\, \Delta t)\, - \,G({t^*}) \,=\, \int\limits_{t_0}^{{t^*} \,+\, \Delta t} {f(t){\rm{d}}t} \, -\, \int\limits_{t_0}^{t^*} {f(t){\rm{d}}t} \, =\, \int\limits_{t^*}^{{t^*}\, +\, \Delta t} {f(t){\rm{d}}t} ,</latex> | ||
| + | |||
in da je iskan odvod možno izraziti takole: | in da je iskan odvod možno izraziti takole: | ||
| + | |||
<latex>G^\prime \, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{G({t^*} \,+\, \Delta t)\, -\, G(t)}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{1}{\Delta t}\int\limits_{t^*}^{{t^*} \,+\, \Delta t} {f(t){\rm{d}}t} .</latex> | <latex>G^\prime \, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{G({t^*} \,+\, \Delta t)\, -\, G(t)}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{1}{\Delta t}\int\limits_{t^*}^{{t^*} \,+\, \Delta t} {f(t){\rm{d}}t} .</latex> | ||
| + | |||
Preostali določen integral se naslavlja na kar najkrajši interval Δ''t''; če je tako, ustreza približni vrednosti integrala morda že kar produkt ''f''(''t''<sup>*</sup> + Δ''t'') Δ''t'', če je le Δ''t'' dovolj majhen. Sledi odgovor: | Preostali določen integral se naslavlja na kar najkrajši interval Δ''t''; če je tako, ustreza približni vrednosti integrala morda že kar produkt ''f''(''t''<sup>*</sup> + Δ''t'') Δ''t'', če je le Δ''t'' dovolj majhen. Sledi odgovor: | ||
| + | |||
<latex>G^\prime \, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{G({t^*}\, +\, \Delta t) \,-\, G(t)}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{f({t^*}\, +\, \Delta t)\Delta t}{\Delta t} \,=\, \mathop {\lim }\limits_{\Delta t \to 0} f({t^*}\, +\, \Delta t) \,=\, f({t^*}).</latex> | <latex>G^\prime \, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{G({t^*}\, +\, \Delta t) \,-\, G(t)}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{f({t^*}\, +\, \Delta t)\Delta t}{\Delta t} \,=\, \mathop {\lim }\limits_{\Delta t \to 0} f({t^*}\, +\, \Delta t) \,=\, f({t^*}).</latex> | ||
| + | |||
Odvod funkcije ''G'' v ''t''<sup>*</sup> je enak funkcijski vrednosti funkcije ''f'' v ''t''<sup>*</sup>, pri tem pa je ''t''<sup>*</sup> ∈ [''t''<sub>0</sub>, ''t''<sub>1</sub>]. Izkoristimo priložnost in izpostavimo glavne lastnosti določnega integrala kot funkcije zgornje meje: | Odvod funkcije ''G'' v ''t''<sup>*</sup> je enak funkcijski vrednosti funkcije ''f'' v ''t''<sup>*</sup>, pri tem pa je ''t''<sup>*</sup> ∈ [''t''<sub>0</sub>, ''t''<sub>1</sub>]. Izkoristimo priložnost in izpostavimo glavne lastnosti določnega integrala kot funkcije zgornje meje: | ||
| + | |||
<latex>{G({t^*})\, =\, \int\limits_{t_0}^{t^*} {f(t){\rm{d}}t} \,\,\,\,\,{\rm{ }} \Rightarrow\,\,\,\,\, {\rm{ }}G({t_0})\, =\, 0\,\,\,\,\,{\rm{ in }}\,\,\,\,\,G({t_1}) \,=\, \int\limits_{t_0}^{t_1} {f(t){\rm{d}}t}\,\,\,\,\, {\rm{ ter }}\,\,\,\,\,G^\prime (t)\, =\, f(t).}</latex> | <latex>{G({t^*})\, =\, \int\limits_{t_0}^{t^*} {f(t){\rm{d}}t} \,\,\,\,\,{\rm{ }} \Rightarrow\,\,\,\,\, {\rm{ }}G({t_0})\, =\, 0\,\,\,\,\,{\rm{ in }}\,\,\,\,\,G({t_1}) \,=\, \int\limits_{t_0}^{t_1} {f(t){\rm{d}}t}\,\,\,\,\, {\rm{ ter }}\,\,\,\,\,G^\prime (t)\, =\, f(t).}</latex> | ||
| + | |||
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 19:26, 12. julij 2010
Ali znamo reči kaj o odvodu funkcije G v točki t* oziroma o limiti naslednjega kvocienta:
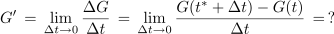
Iz lastnosti integrala izhaja, da je števec v resnici določen integral funkcije f od t* do t* + Δt, saj je
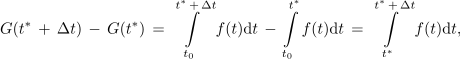
in da je iskan odvod možno izraziti takole:
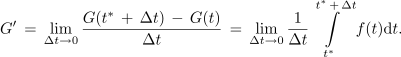
Preostali določen integral se naslavlja na kar najkrajši interval Δt; če je tako, ustreza približni vrednosti integrala morda že kar produkt f(t* + Δt) Δt, če je le Δt dovolj majhen. Sledi odgovor:
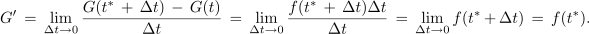
Odvod funkcije G v t* je enak funkcijski vrednosti funkcije f v t*, pri tem pa je t* ∈ [t0, t1]. Izkoristimo priložnost in izpostavimo glavne lastnosti določnega integrala kot funkcije zgornje meje:
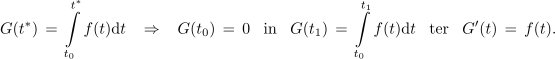
| | 5.5 Nedoločen integral funkcije |
