Iz e-ELEKTROTEHNIKA plus
m (1 revision) |
|||
| Vrstica 1: | Vrstica 1: | ||
| - | Polnilno vezje sestavljajo napetostni vir, stikalo, upor in tuljava (slika 8). Trenutek vklopa | + | Polnilno vezje sestavljajo napetostni vir, stikalo, upor in tuljava (slika 8). Trenutek vklopa naj bo ''t''<sub>0</sub> = 0 s. Pred tem je vezje »mrtvo«, toka ni in tuljava je brez energije. Tik po vklopu je tok v zanki še vedno enak nič (saj se v tuljavi, v kateri ga prej ni bilo, ne more kar pojaviti). To pomeni, da je prvi hip tudi napetost na uporu enaka nič in da je napetost vira v celotni na tuljavi. Če pa je, potem ima odvod toka v začetku vrednost d''i'' / d''t'' = ''u<sub>L</sub>'' / ''L'', zaradi katere začneta tok in napetost na uporu naraščati, napetost na tuljavi pa upadati. Ker je ta vse manjša, se upočasnjuje tudi naraščanje toka. Po daljšem času doseže največjo vrednost, določata pa jo napetost vira in upornost upora. Tok se ne spreminja več, napetost na tuljavi je enaka nič in napetost na uporu je enaka napetosti vira. |
| - | Povedano pretvorimo v izraze | + | Povedano pretvorimo v izraze. Napišimo zančno enačbo za poljuben trenutek ''t'' po vklopu stikala in izrazimo napetosti na uporu in tuljavi: |
<latex>t\,\, \textgreater\,\, {t_0}\,:\,\,\,{\rm{ }} - \,U \,+ \,{u_R} \,+\, {u_L}\, =\, 0{\rm{ \,\,\,\,\, in\,\,\,\,\, }}{u_R}\, =\, Ri{\rm{ \,\,\,\,\,ter\,\,\,\,\, }}{u_L}\, =\,L\frac{{\rm{d}}i}{{\rm{d}}t}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }} \,-\, U\, +\, Ri\, +\, {u_L} \,=\, 0.</latex> | <latex>t\,\, \textgreater\,\, {t_0}\,:\,\,\,{\rm{ }} - \,U \,+ \,{u_R} \,+\, {u_L}\, =\, 0{\rm{ \,\,\,\,\, in\,\,\,\,\, }}{u_R}\, =\, Ri{\rm{ \,\,\,\,\,ter\,\,\,\,\, }}{u_L}\, =\,L\frac{{\rm{d}}i}{{\rm{d}}t}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }} \,-\, U\, +\, Ri\, +\, {u_L} \,=\, 0.</latex> | ||
Redakcija: 09:50, 8. junij 2010
Polnilno vezje sestavljajo napetostni vir, stikalo, upor in tuljava (slika 8). Trenutek vklopa naj bo t0 = 0 s. Pred tem je vezje »mrtvo«, toka ni in tuljava je brez energije. Tik po vklopu je tok v zanki še vedno enak nič (saj se v tuljavi, v kateri ga prej ni bilo, ne more kar pojaviti). To pomeni, da je prvi hip tudi napetost na uporu enaka nič in da je napetost vira v celotni na tuljavi. Če pa je, potem ima odvod toka v začetku vrednost di / dt = uL / L, zaradi katere začneta tok in napetost na uporu naraščati, napetost na tuljavi pa upadati. Ker je ta vse manjša, se upočasnjuje tudi naraščanje toka. Po daljšem času doseže največjo vrednost, določata pa jo napetost vira in upornost upora. Tok se ne spreminja več, napetost na tuljavi je enaka nič in napetost na uporu je enaka napetosti vira.
Povedano pretvorimo v izraze. Napišimo zančno enačbo za poljuben trenutek t po vklopu stikala in izrazimo napetosti na uporu in tuljavi:
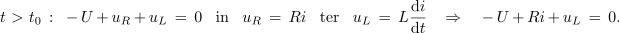
Nadaljujemo z odvajajem zadnje enačbe:
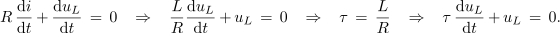
Časovni konstanti τ ustreza tokrat kvocient L / R. Možno rešitev za napetost na tuljavi iščemo spet v obliki produkta konstante in eksponentne funkcije:
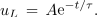
Rekli smo, da je tok tik po vklopu še vedno enak nič:
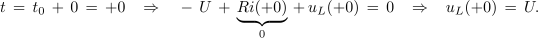
Tik po vklopu stikala je napetost tuljave enaka napetosti vira. Sledi:
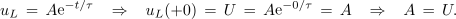
Napetost tuljave določa funkcija
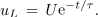
Iz nje sledita še napetost na uporu in tok v zanki (slika 9):
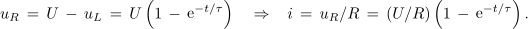
Ob polnjenju se v tuljavi kopiči magnetna energija,
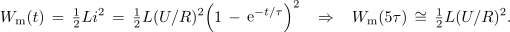
Po petih časovnih konstantah se bo v magnetnem polju tuljave akumulirala praktično že vsa možna energija. V uporu se sprošča joulska toplota z močjo Ri2 še tudi kasneje, ko prehodni pojav že v celoti izzveni.
| | 5.11 Izklop tuljave |
