Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
| Vrstica 7: | Vrstica 7: | ||
| - | <latex>{\omega _{\rm{r}}}L\, =\, \frac{1}{{\omega _{\rm{r}}}C}</latex> | + | <latex>{\omega _{\rm{r}}}L\, =\, \frac{1}{{\omega _{\rm{r}}}C}</latex> oziroma <latex>2\pi \,{f_{\rm{r}}}L \,= \,\frac{1}{2\pi {f_{\rm{r}}}C}</latex> in od tod <latex>{f_{\rm{r}}} \,= \,\frac{1}{2\pi \sqrt {LC} }|||(Hz)</latex> |
| - | + | ||
| - | + | ||
| - | oziroma | + | |
| - | + | ||
| - | + | ||
| - | <latex>2\pi \,{f_{\rm{r}}}L \,= \,\frac{1}{2\pi {f_{\rm{r}}}C}</latex> | + | |
| - | + | ||
| - | + | ||
| - | in od tod | + | |
| - | + | ||
| - | + | ||
| - | <latex>{f_{\rm{r}}} \,= \,\frac{1}{2\pi \sqrt {LC} }|||(Hz)</latex> | + | |
Redakcija: 19:33, 25. maj 2010
- Frekvenco vsiljenega nihanja, pri kateri je amplituda nihanja energije v zaporednem nihajnem krogu bistveno večja kot pri drugih frekvencah, imenujemo resonančna[1] frekvenca (fr).
Resonančno frekvenco izračunamo iz enakosti reaktanc nihajnega kroga pri resonančni frekvenci:
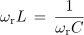
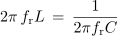
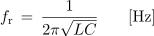
- Resonančna frekvenca zaporednega nihajnega kroga je obratno sorazmerna z geometrično sredino induktivnosti L in kapacitivnosti kroga C (√LC).
Resonančna frekvenca vsiljenega nihanja je enaka frekvenci lastnega nihanja nedušenega nihajnega kroga, enačbo za računanje frekvence lastnega oziroma vsiljenega resonančnega nihanja pa imenujemo Thomsonova[2] enačba.
Izračunajmo resonančno frekvenco nihajnega kroga iz poskusa 7.3.1:
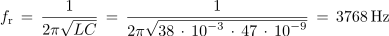
Za zaporedni nihajni krog pri f = fr torej velja:
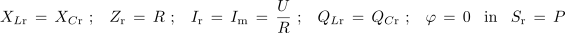
Opombe
- ↑ resonare, lat. = odmevati, skupaj nihati
- ↑ Thomson William, Lord Kelvin, angleški fizik, 1824 – 1907
 7.3.1 Zaporedni električni nihajni krog
| 7.3.1.2 Kakovost zaporednega nihajnega kroga
|
