Iz e-ELEKTROTEHNIKA plus
(Nova stran z vsebino: Odvoda konstantne in linearne funkcije smo že osvetlili. Naslednja naj bo morda kar funkcija ''f''(''t'') = ''t''<sup>3</sup>, njen odvod najdemo po definiciji: <latex>\matho…) |
|||
| Vrstica 1: | Vrstica 1: | ||
Odvoda konstantne in linearne funkcije smo že osvetlili. Naslednja naj bo morda kar funkcija ''f''(''t'') = ''t''<sup>3</sup>, njen odvod najdemo po definiciji: | Odvoda konstantne in linearne funkcije smo že osvetlili. Naslednja naj bo morda kar funkcija ''f''(''t'') = ''t''<sup>3</sup>, njen odvod najdemo po definiciji: | ||
| + | |||
<latex>\mathop {\lim }\limits_{\Delta t \to 0} \frac{\Delta f}{\Delta t} \,= \,\mathop {\lim }\limits_{\Delta t \to 0} \frac{{{(t\, +\, \Delta t)}^3} \,- \,{t^3}}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{{t^3}\, +\, 3{t^2}\Delta t \,+\, 3t{{(\Delta t)}^2}\, +\, {{(\Delta t)}^3} \,-\, {t^3}}{\Delta t}\, =\, </latex> | <latex>\mathop {\lim }\limits_{\Delta t \to 0} \frac{\Delta f}{\Delta t} \,= \,\mathop {\lim }\limits_{\Delta t \to 0} \frac{{{(t\, +\, \Delta t)}^3} \,- \,{t^3}}{\Delta t}\, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{{t^3}\, +\, 3{t^2}\Delta t \,+\, 3t{{(\Delta t)}^2}\, +\, {{(\Delta t)}^3} \,-\, {t^3}}{\Delta t}\, =\, </latex> | ||
| + | |||
<latex>\mathop {\lim }\limits_{\Delta t \to 0} \left( {3{t^2} \,+ \,3t\Delta t\, +\, {{(\Delta t)}^2}} \right).</latex> | <latex>\mathop {\lim }\limits_{\Delta t \to 0} \left( {3{t^2} \,+ \,3t\Delta t\, +\, {{(\Delta t)}^2}} \right).</latex> | ||
| + | |||
Ko Δ''t'' stremi k nič, se zadnja dva sumanda manjšata in postajata neznatna do prvega, zato je: | Ko Δ''t'' stremi k nič, se zadnja dva sumanda manjšata in postajata neznatna do prvega, zato je: | ||
| + | |||
<latex>\frac{{\rm{d}}f}{{\rm{d}}t} \,=\, f^\prime \, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{\Delta f}{\Delta t} \,= \,\mathop {\lim }\limits_{\Delta t \to 0} \left( {3{t^2}\, +\, 3t\Delta t \,+\, {{(\Delta t)}^2}} \right)\, =\, 3{t^2}.</latex> | <latex>\frac{{\rm{d}}f}{{\rm{d}}t} \,=\, f^\prime \, =\, \mathop {\lim }\limits_{\Delta t \to 0} \frac{\Delta f}{\Delta t} \,= \,\mathop {\lim }\limits_{\Delta t \to 0} \left( {3{t^2}\, +\, 3t\Delta t \,+\, {{(\Delta t)}^2}} \right)\, =\, 3{t^2}.</latex> | ||
| + | |||
Odvod funkcije ''t''<sup>3</sup> je funkcija 3''t''<sup>2</sup>, na podoben način bi izvedli odvod potenčne funkcije ''n''-te stopnje. Dobili bi: | Odvod funkcije ''t''<sup>3</sup> je funkcija 3''t''<sup>2</sup>, na podoben način bi izvedli odvod potenčne funkcije ''n''-te stopnje. Dobili bi: | ||
| + | |||
<latex>{f(t) \,=\, {t^n}{\rm{ }}\,\,\,\,\, \Rightarrow {\rm{ }}\,\,\,\,\,f^\prime (t) \,=\, \left( {t^n} \right)^\prime \, =\, n{t^{n \,-\, 1}}.}</latex> | <latex>{f(t) \,=\, {t^n}{\rm{ }}\,\,\,\,\, \Rightarrow {\rm{ }}\,\,\,\,\,f^\prime (t) \,=\, \left( {t^n} \right)^\prime \, =\, n{t^{n \,-\, 1}}.}</latex> | ||
| + | |||
Pravilo je: Eksponent potenčne funkcije se zmanjša za ena, prvotni pa se kot multiplikator seli pred novo potenčno funkcijo. Povsem enako pravilo velja tudi pri funkcijah necelih eksponentov. | Pravilo je: Eksponent potenčne funkcije se zmanjša za ena, prvotni pa se kot multiplikator seli pred novo potenčno funkcijo. Povsem enako pravilo velja tudi pri funkcijah necelih eksponentov. | ||
| + | |||
Sedaj pa še nedoločen integral oziroma ''F''(''t'') funkcije ''f''(''t'') = ''t''<sup>3</sup>. Funkcija ''F''(''t'') je enaka vsoti četrtine potenčne funkcije četrte stopnje in poljubne konstante: | Sedaj pa še nedoločen integral oziroma ''F''(''t'') funkcije ''f''(''t'') = ''t''<sup>3</sup>. Funkcija ''F''(''t'') je enaka vsoti četrtine potenčne funkcije četrte stopnje in poljubne konstante: | ||
| + | |||
<latex>f(t) \,= \,{t^3}{\rm{ }} \,\,\,\,\,\Rightarrow \,\,\,\,\,{\rm{ }}F(t) \,=\, \int {f(t)} {\rm{d}}t \,=\, \int {t^3} {\rm{d}}t\, =\, \frac{t^4}{4}\, +\,C\,\,,\,\,\,\,\,{\rm{ saj \,je}}</latex> | <latex>f(t) \,= \,{t^3}{\rm{ }} \,\,\,\,\,\Rightarrow \,\,\,\,\,{\rm{ }}F(t) \,=\, \int {f(t)} {\rm{d}}t \,=\, \int {t^3} {\rm{d}}t\, =\, \frac{t^4}{4}\, +\,C\,\,,\,\,\,\,\,{\rm{ saj \,je}}</latex> | ||
| + | |||
<latex>F^\prime (t)\, =\, \left( {\frac{t^4}{4}\, +\, C} \right)^\prime \, =\, \frac{1}{4}\left( {t^4} \right)^\prime\, +\,C^\prime \,= \,\frac{1}{4}\left( {4{t^3}} \right) \,+ \,0 \,= \,{t^3}.</latex> | <latex>F^\prime (t)\, =\, \left( {\frac{t^4}{4}\, +\, C} \right)^\prime \, =\, \frac{1}{4}\left( {t^4} \right)^\prime\, +\,C^\prime \,= \,\frac{1}{4}\left( {4{t^3}} \right) \,+ \,0 \,= \,{t^3}.</latex> | ||
| + | |||
Splošno pravilo je: | Splošno pravilo je: | ||
| + | |||
<latex>{f(t) \,=\, {t^n}\,\,,\,\,\,\,n\, \ne \, - 1{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}F(t) \,= \,\int{t^n} {\rm{d}}t \,=\, \frac{t^{n + 1}}{n\, + \,1} \,+\, C.}</latex> | <latex>{f(t) \,=\, {t^n}\,\,,\,\,\,\,n\, \ne \, - 1{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}F(t) \,= \,\int{t^n} {\rm{d}}t \,=\, \frac{t^{n + 1}}{n\, + \,1} \,+\, C.}</latex> | ||
| Vrstica 28: | Vrstica 40: | ||
'''Zgled 1''' | '''Zgled 1''' | ||
V nekem časovnem intervalu določa tok skozi tuljavo induktivnosti ''L'' izraz ''i'' = ''at''<sup>2</sup> - ''bt'' + ''c''. Izrazimo napetost na tuljavi. ⇒ Izhajamo iz enačbe tuljave: | V nekem časovnem intervalu določa tok skozi tuljavo induktivnosti ''L'' izraz ''i'' = ''at''<sup>2</sup> - ''bt'' + ''c''. Izrazimo napetost na tuljavi. ⇒ Izhajamo iz enačbe tuljave: | ||
| + | |||
<latex>u\, =\, L\frac{{\rm{d}}i}{{\rm{d}}t}\, =\, Li^\prime \, =\, L(a{t^2}\, -\, bt\, +\, c)^\prime \, =\, L(2at \,-\, b).</latex> | <latex>u\, =\, L\frac{{\rm{d}}i}{{\rm{d}}t}\, =\, Li^\prime \, =\, L(a{t^2}\, -\, bt\, +\, c)^\prime \, =\, L(2at \,-\, b).</latex> | ||
| Vrstica 34: | Vrstica 47: | ||
'''Zgled 2.''' | '''Zgled 2.''' | ||
Med časoma ''t''<sub>1</sub> in ''t''<sub>2</sub> podaja tok skozi upor upornosti ''R'' izraz ''i'' = ''at'' - ''b''. Izrazimo množino toplote med tema časoma. ⇒ Sproščeno toploto določa integral moči ''p'' = ''Ri''<sup>2</sup>: | Med časoma ''t''<sub>1</sub> in ''t''<sub>2</sub> podaja tok skozi upor upornosti ''R'' izraz ''i'' = ''at'' - ''b''. Izrazimo množino toplote med tema časoma. ⇒ Sproščeno toploto določa integral moči ''p'' = ''Ri''<sup>2</sup>: | ||
| + | |||
<latex>\int\limits_{t_1}^{t_2} {p{\rm{d}}t} \, =\, \int\limits_{t_1}^{t_2} {R{i^2}{\rm{d}}t}\, =\, R\int\limits_{t_1}^{t_2} {{{\left( {at \,- \,b} \right)}^2}{\rm{d}}t} \, =\, R\int\limits_{t_1}^{t_2} {\left( {{a^2}{t^2} \,- \,2abt \,+ \,{b^2}} \right){\rm{d}}t} \, =\, </latex> | <latex>\int\limits_{t_1}^{t_2} {p{\rm{d}}t} \, =\, \int\limits_{t_1}^{t_2} {R{i^2}{\rm{d}}t}\, =\, R\int\limits_{t_1}^{t_2} {{{\left( {at \,- \,b} \right)}^2}{\rm{d}}t} \, =\, R\int\limits_{t_1}^{t_2} {\left( {{a^2}{t^2} \,- \,2abt \,+ \,{b^2}} \right){\rm{d}}t} \, =\, </latex> | ||
| + | |||
<latex>R\left( {\frac{{a^2}{t^3}}{3} \,-\, ab{t^2} \,+\, {b^2}t\, +\, C} \right)_{t_1}^{t_2}\, =\, R\left( {\frac{{a^2}t_2^3}{3} \,-\, \frac{{a^2}t_1^3}{3}\, -\, abt_2^2 \,+\, abt_1^2\, +\, {b^2}{t_2} \,-\, {b^2}{t_1}} \right).</latex> | <latex>R\left( {\frac{{a^2}{t^3}}{3} \,-\, ab{t^2} \,+\, {b^2}t\, +\, C} \right)_{t_1}^{t_2}\, =\, R\left( {\frac{{a^2}t_2^3}{3} \,-\, \frac{{a^2}t_1^3}{3}\, -\, abt_2^2 \,+\, abt_1^2\, +\, {b^2}{t_2} \,-\, {b^2}{t_1}} \right).</latex> | ||
Trenutna redakcija s časom 19:32, 12. julij 2010
Odvoda konstantne in linearne funkcije smo že osvetlili. Naslednja naj bo morda kar funkcija f(t) = t3, njen odvod najdemo po definiciji:
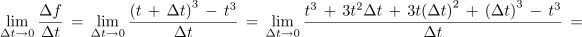
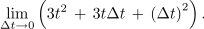
Ko Δt stremi k nič, se zadnja dva sumanda manjšata in postajata neznatna do prvega, zato je:
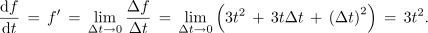
Odvod funkcije t3 je funkcija 3t2, na podoben način bi izvedli odvod potenčne funkcije n-te stopnje. Dobili bi:
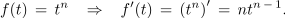
Pravilo je: Eksponent potenčne funkcije se zmanjša za ena, prvotni pa se kot multiplikator seli pred novo potenčno funkcijo. Povsem enako pravilo velja tudi pri funkcijah necelih eksponentov.
Sedaj pa še nedoločen integral oziroma F(t) funkcije f(t) = t3. Funkcija F(t) je enaka vsoti četrtine potenčne funkcije četrte stopnje in poljubne konstante:
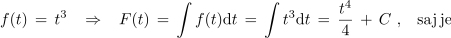
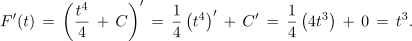
Splošno pravilo je:
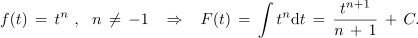
Zgled 1
V nekem časovnem intervalu določa tok skozi tuljavo induktivnosti L izraz i = at2 - bt + c. Izrazimo napetost na tuljavi. ⇒ Izhajamo iz enačbe tuljave:
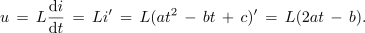
Zgled 2.
Med časoma t1 in t2 podaja tok skozi upor upornosti R izraz i = at - b. Izrazimo množino toplote med tema časoma. ⇒ Sproščeno toploto določa integral moči p = Ri2:
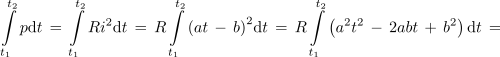
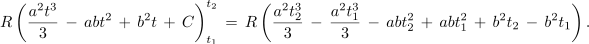
| | 5.7.2 Harmonična funkcija. |
