Iz e-ELEKTROTEHNIKA plus
(Nova stran z vsebino: Z njeno strmino, ki preide v limiti v odvod, smo se že spopadli. Takrat smo to opravili na geometrijski način, tokrat pa takole<ref>Iz matematike vemo, da je <latex>\mathop {…)
Trenutna redakcija s časom 12:46, 27. junij 2010
Z njeno strmino, ki preide v limiti v odvod, smo se že spopadli. Takrat smo to opravili na geometrijski način, tokrat pa takole[1]:
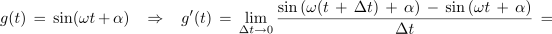
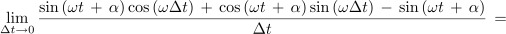
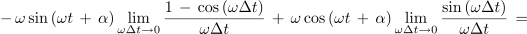
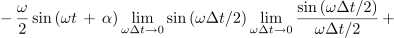
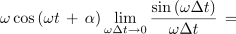
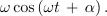
Če bi podobno postopali tudi pri kosinusni funkciji, bi dobili:
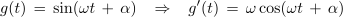
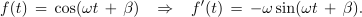
Iz odvodov razberemo pravili. Odvod sinusne je kosinusna funkcija in odvod kosinusne je negativna sinusna funkcija. Pri odvodih se konstanta ω prenese iz argumenta v multiplikator s funkcijo. Za harmonični funkciji lahko brž najdemo še nedoločena integrala:
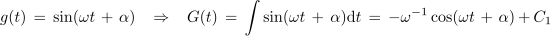
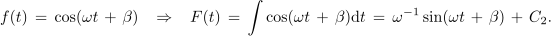
Zgled 3
Pri analizi harmonično vzbujanih reaktivnih elementov smo ugotovili, da je moč dotekanja energije v njih harmonična časovna funkcija, katere amplituda ustreza jalovi moči Q. Trenutno moč p(t) naj določa izraz Qsin(2ωt), v katerem je ω krožna frekvenca toka oziroma napetosti. V prvi četrtini periode toka (napetosti) je moč pozitivna in element se polni, drugo četrtino periode se element prazni itn. V trenutku t0 = 0 s naj bo element brez energije, W(t0) = 0 J. Določimo energijo v elementu v kasnejšem času t1. ⇒ Moč je odvod energije, zato veljajo zveze:
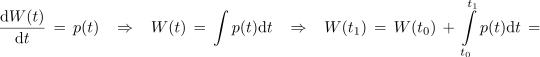
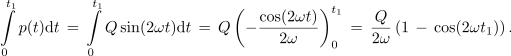
Največja energija je v elementu takrat, ko ima kosinusna funkcija vrednost -1; enaka je Q / ω. Poprečna energija je polovica tega, torej Q / 2ω. Če ima tuljava jalovo moč 2 kvar, bo pri 50 Hz poprečna energija v njej 3,18 J, največja pa 6,36 J. Slednja je sicer majhna, vendar se moramo zavedati, da je v eni sekundi pride ali odide stokrat toliko.
Opombe
- ↑ Iz matematike vemo, da je
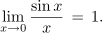
| | 5.7.3 Eksponentna funkcija |
