Iz e-ELEKTROTEHNIKA plus
(Nova stran z vsebino: Označevanje simbola idealnega transformatorja. Obravnavani transformator je bil idealiziran, brez izgub in popolno skloplje…) |
|||
| Vrstica 1: | Vrstica 1: | ||
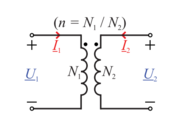
| - | [[Slika: | + | [[Slika:eele_slika_visji_067.svg|thumb|Slika 67: Označevanje simbola idealnega transformatorja. ]] |
| - | Obravnavani transformator je bil idealiziran, brez izgub in popolno sklopljenih navitij, idealni pa bi bil tisti, katerega jedro bi imelo neskončno permeabilnost (''R''m = 0) oziroma neskončne induktivnosti, da bi bila nična tako magnetilni tok kot moč za magnetenje jedra. Podatek idealnega transformatorja sta v tem primeru števili ''N''<sub>1</sub> in ''N''<sub>2</sub> oziroma razmerje ''n''. Električni simbol idealnega transformatorja je identičen prejšnjemu, le da impedance smiselno zamenjata števili ovojev (slika | + | Obravnavani transformator je bil idealiziran, brez izgub in popolno sklopljenih navitij, idealni pa bi bil tisti, katerega jedro bi imelo neskončno permeabilnost (''R''m = 0) oziroma neskončne induktivnosti, da bi bila nična tako magnetilni tok kot moč za magnetenje jedra. Podatek idealnega transformatorja sta v tem primeru števili ''N''<sub>1</sub> in ''N''<sub>2</sub> oziroma razmerje ''n''. Električni simbol idealnega transformatorja je identičen prejšnjemu, le da impedance smiselno zamenjata števili ovojev (slika 67). Njegovi enačbi sta v resnici le dve, napetostna in tokovna: |
Trenutna redakcija s časom 18:43, 12. julij 2010
Obravnavani transformator je bil idealiziran, brez izgub in popolno sklopljenih navitij, idealni pa bi bil tisti, katerega jedro bi imelo neskončno permeabilnost (Rm = 0) oziroma neskončne induktivnosti, da bi bila nična tako magnetilni tok kot moč za magnetenje jedra. Podatek idealnega transformatorja sta v tem primeru števili N1 in N2 oziroma razmerje n. Električni simbol idealnega transformatorja je identičen prejšnjemu, le da impedance smiselno zamenjata števili ovojev (slika 67). Njegovi enačbi sta v resnici le dve, napetostna in tokovna:
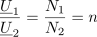
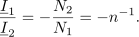
Razmerje napetosti določa prestavno razmerje, razmerje protifaznih tokov pa recipročna vrednost prestavnega razmerja. Ko idealni transformator povezuje breme z virom, veljata še enačbi:[1]
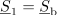
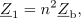
da sta vhodni in izhodni kompleksni moči enaki in da se impedanca bremena transformira na vhod s kvadratom prestave.
Opombe
- ↑ S pomočjo idealnega transformatorja moremo oblikovati še drugačno nadomestno vezje brezizgubnega transformatorja: vzporedno k primarnemu navitju idealnega transformatorja pridružimo tuljavo z induktivnostjo primarnega navitja. Primarni tok se v tem primeru deli v magnetilni skozi tuljavo in v ravnotežni skozi primar idealnega transformatorja (torej v smislu izraza za primarni tok).
| | 3.7.9 Uporaba transformatorja |