Iz e-ELEKTROTEHNIKA plus
| Vrstica 176: | Vrstica 176: | ||
Pri praznjenju kondenzatorja na način, ki ga prikazuje slika 6.1.3, se tudi v električnem polju kondenzatorja shranjena energija v obliki toplote prek iste ohmske upornosti ''R'' sprosti iz električnega kroga. | Pri praznjenju kondenzatorja na način, ki ga prikazuje slika 6.1.3, se tudi v električnem polju kondenzatorja shranjena energija v obliki toplote prek iste ohmske upornosti ''R'' sprosti iz električnega kroga. | ||
| + | |||
| + | |||
| + | <animacija>eele_animacija_010_prehodni_pojav_RC.swf|Prehodni pojavi v RC električnem krogu</animacija> | ||
| + | |||
<primer> | <primer> | ||
| Vrstica 202: | Vrstica 206: | ||
<latex>t \,=\, 0\,\,\,\,\, \to \,\,\,\,\,i\, =\, \frac{U}{R}\, = \,\frac{6}{455} \,= \,12\,{\rm{mA}}</latex> | <latex>t \,=\, 0\,\,\,\,\, \to \,\,\,\,\,i\, =\, \frac{U}{R}\, = \,\frac{6}{455} \,= \,12\,{\rm{mA}}</latex> | ||
</primer> | </primer> | ||
| - | |||
| - | |||
| - | |||
Trenutna redakcija s časom 18:02, 4. september 2010
![](javascript: loadPicture("Eele_slika_6_1_1.svg", 1674);)
Poskus 6.1.1:
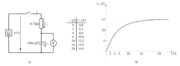
Zaporedno vezavo upora z upornostjo 4,4 kΩ in kondenzatorja s kapacitivnostjo 1000 μF priključimo prek stikala na izvor enosmerne napetosti npr. 15 V (sl. 6.1.1 a).
Od trenutka vklopa stikala (t = 0) spremljamo potek spreminjanja napetosti na kondenzatorju z odčitavanjem V-metra v časih, ki so podani v preglednici (sl. 6.1.1 b).
- Napetost na kondenzatorju narašča od 0 V in se šele po več kot 20 sekundah ustali približno na napetosti izvora.
![](javascript: loadPicture("Eele_foto_132.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_131.jpg", 533);)
V trenutku vklopa, ko je kondenzator še ni naelektren, med oblogama kondenzatorja ni napetosti, ki bi nasprotovala polnjenju kondenzatorja. V trenutku vklopa je zato celotna napetost izvora na ohmskem uporu R, začetni tok polnjenja kondenzatorja pa je določen z napetostjo izvora in ohmsko upornostjo.
- Prazen kondenzator pomeni v trenutku priključitve na enosmerno napetost kratek stik.
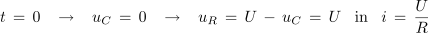
Po določenem času se kondenzator naelektri z elektrino Q = C • U, napetost na kondenzatorju pa se izenači z napetostjo izvora. Nadaljnje elektrenje kondenzatorja ni več mogoče, zato tok v krogu preneha teči:
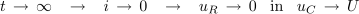
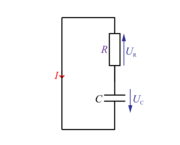
Zakonitost spreminjanja napetosti na kondenzatorju in ostalih električnih količin kroga med obema stacionarnima stanjema dobimo iz enačbe napetostne zanke:
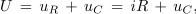
ki jo z upoštevanjem izraza za tok polnjenja kondenzatorja
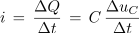
preoblikujemo v
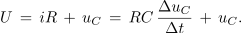
Iz dobljene enačbe je razvidno, da je padec napetosti na uporu premo sorazmeren s hitrostjo spreminjanja napetosti na kondenzatorju. Vemo, da je ta največja na samem začetku polnjenja kondenzatorja.
Za nadaljnje razvijanje dobljene enačbe nimamo potrebnega znanja matematike, zato se z rešitvijo enačbe[1] le seznanimo:
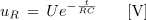
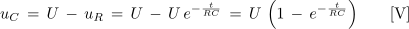
- Količine se v prehodnem pojavu spreminjajo po eksponetni zakonitosti.
Člen e(-t/RC) v enačbah odraža naravno zakonitost časovnega poteka prehodnih pojavov pri padcih napetosti na uporu in kondenzatorju. To je splošna zakonitost in velja tudi za druge vrste prehodnih pojavov. Preverimo dobljeni enačbi na začetnih in končnih vrednostih prehodnega pojava iz poskusa 6.1.1:
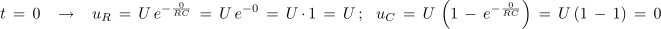
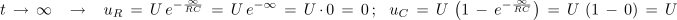
- Po priključitvi zaporedne vezave upora in kondenzatorja na enosmerno napetost narašča napetost na kondenzatorju uC od 0 V na napetost izvora po eksponentni zakonitosti.
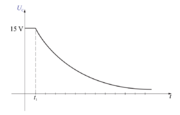
- Po priključitvi zaporedne RC vezave na enosmerno napetost pada napetost na uporu od napetosti izvora proti 0 V po eksponentni zakonitosti.
Tok v krogu v času polnjenja kondenzatorja je premo sorazmeren z napetostjo na uporu:
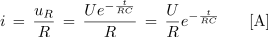
Preverimo začetni in končni tok:
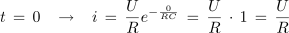
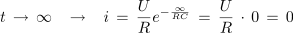
- Tok polnjenja kondenzatorja pada od začetne vrednosti U /R proti nič po eksponentni zakonitosti.
V imenovalcu eksponenta vseh izrazov količin v prehodnem pojavu je produkt RC. Poglejmo, čemu je enak produkt pripadajočih enot:
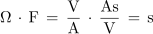
Produkt RC ima dimenzijo časa. Imenujemo ga časovna konstanta prehodnega pojava (τ).
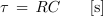
Vstavimo v enačbo prehodnega pojava, npr. napetosti na kondenzatorju in uporu čas t, ki je enak časovni konstanti prehodnega pojava τ:
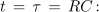
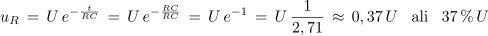
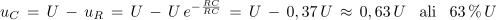
- Po času t = τ vrednost količin v prehodnem pojavu naraste na 63 % končne vrednosti ali pade na 37 % začetne vrednosti.
Čeprav prehodni pojav izzveni šele po času t → ∞, pa računsko in tudi z merjenjem (poskus 6.1.1) lahko ugotovimo, da se prehodni pojav praktično konča po času ≈ 5τ , ko vrednost količine v prehodnem pojavu naraste na praktično 99,5 % končne ali pade na 0,5 % začetne vrednosti.
- Prehodni pojavi trajajo tpp ≈ 5 τ .
- Trajanje prehodnih pojavov v RC krogih je praktično premo sorazmerno z upornostjo upora R in kapacitivnostjo kondenzatorja C.
Podobno kot pri polnjenju bi dobili enačbe časovnih potekov količin v prehodnem pojavu pri praznjenju kondenzatorja prek upornosti R (slika 6.1.2). Ker je bil kondenzator naelektren, ima pri praznjenju po sliki 6.1.3 vlogo izvora napetosti, ki poganja tok v električnem krogu v obratni smeri kot pri polnjenju. Napetosti na kondenzatorju in uporu sta si do izpraznitve kondenzatorja po velikosti enaki in nasprotno usmerjeni.
![](javascript: loadPicture("Eele_slika_6_1_2.svg", 508);)
![](javascript: loadPicture("Eele_slika_6_1_3.svg", 800);)
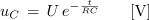
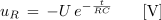
in
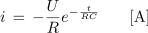
Zaradi boljše preglednosti nad ugotovljenim povzemimo značilnosti prehodnih pojavov v RC krogih s sliko 6.1.4.
![](javascript: loadPicture("Eele_slika_6_1_4.svg", 900);)
Poglejmo še, kaj se v prehodnem pojavu dogaja z energijo. Pri polnjenju kondenzatorja se del energije, ki odteka iz generatorja, na ohmski upornosti R pretvarja v toplotno energijo in sprošča iz električnega kroga, drugi del pa se kopiči v električnem polju kondenzatorja. V času polnjenja kondenzatorja odteče tako iz generatorja energija:
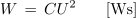
kondenzator pa od te, zaradi delne pretvorbe v toploto, shrani le polovico:
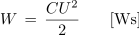
Pri praznjenju kondenzatorja na način, ki ga prikazuje slika 6.1.3, se tudi v električnem polju kondenzatorja shranjena energija v obliki toplote prek iste ohmske upornosti R sprosti iz električnega kroga.
Primer:
Zaporedno vezavo upora z upornostjo 2 kΩ in kondenzatorja s kapacitivnostjo 4,7 μF priključimo na enosmerno napetost 12 V. Izračunaj časovno konstanto in čas trajanja prehodnega pojava v krogu ter napetost na kondenzatorju po času τ in 20 ms.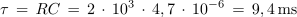
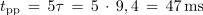
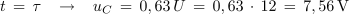
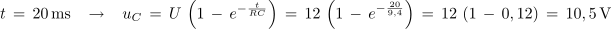
Primer:
Kolikšna mora biti upornost upora zaporedno vezanega s kondenzatorjem, katerega kapacitivnost je 1 μF, če želimo, da napetost na uporu po 0,5 ms po priključitvi vezave na enosmerno napetost 6 V, pade na 2 V? Kolikšen je tok ob vklopu?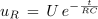
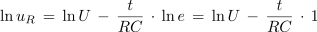
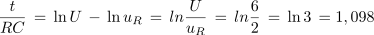
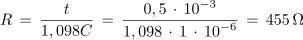
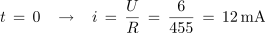
Opombe
- ↑ diferencialna enačba, področje višje matematike
 6.1 Prehodni pojavi v krogu z uporom in kondenzatorjem
| 6.1.2 Neželeni učinki RC prehodnih pojavov
|
