5.5 Nedoločen integral funkcije

Iz e-ELEKTROTEHNIKA plus

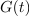
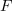
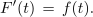
Funkcijo smo definirali in poznamo njene lastnosti, ostaja pa še naloga, kako do nje priti, kako jo najti? Iskanje začnimo s funkcijo , od katere terjamo, da zadošča enačbi

Z združitvijo te s podobno za G sledi:

Odvod razlike funkcij je enak nič; ker pa je odvod konstante tudi enak nič, se zgornji funkciji razlikujeta kvečjemu za konstanto, npr. za konstanto :

Iz lastnosti sledi konstanta , kar končno dá:

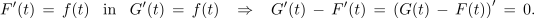
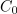
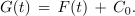
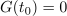
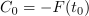
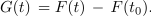
Funkciji F, ki zadošča enačbi F′ = f, rečemo nedoločen integral funkcije f; to zapisujemo v naslednjih enakovrednih oblikah:

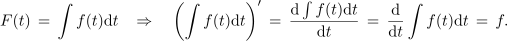
Pridevnik »nedoločen« stoji zato, ker se funkcija F od funkcije G, od funkcije zgornje meje določenega integrala, razlikuje za aditivno konstanto. Zapis F(t) = ∫f(t)dt bi mogli razumeti tudi kot nekakšno nedoločeno vsoto paketov f(t)dt, kateri bi mogli brez škode prišteli poljubno konstanto. Nadalje vidimo, da je iskanje nedoločenega integrala F funkcije f opravilo, ki je obratno odvajanju: iskanje funkcije F ustreza iskanju tiste funkcije, katere odvod je funkcija f.

5.4.2 Odvod funkcije zgornje meje določenega integrala

5.6 Zveza med določenim in nedoločenim integralom