Iz e-ELEKTROTEHNIKA plus
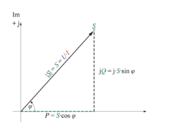
Če trikotnik moči poljubne vezave upora, tuljave in/ali kondenzatorja narišemo v kompleksno ravnino (slika 3.4.18), lahko ugotovimo:
- Navidezno moč izmeničnega toka je v kompleksni ravnini ponazorjena s kompleksorjem S, katerega realna komponenta je delovna moč P, imaginarna komponenta pa jalova moč jQ.
Jalova moč ima lahko pri tem induktivni (jQL) ali kapacitivni (- jQC) značaj. V algebrski obliki zapišemo kompleksor moči S:
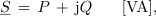
v eksponentni obliki pa
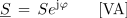
Pri računanju moči v eksponentni kompleksni obliki pa moramo biti previdni. Poglejmo:
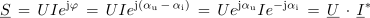
ali
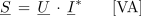
- Kompleksor moči S izmeničnega toka je določen s produktom kompleksorja napetosti U in konjugiranega kompleksorja toka I*.
Problem bi sicer lahko pričakovali, saj v istem kazalčnem diagramu lahko enakovredno obravnavamo le sinusne količine enakih frekvenc. Obravnavana navidezna moč pa je sestavljena iz delovne in izmenične jalove komponente, ki ima dvojno frekvenco toka oziroma napetosti.
Če upoštevamo še Ohmov zakon, ki velja tudi v kompleksni obliki U = I • Z, lahko izmenično moč računamo tudi v obliki:
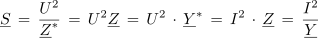
Primera:
Primer:
1. Izračunaj navidezno, delovno in jalovo moč izmeničnega toka pri podatkih U = 230 V, αU = 78 º, I = 2 A in αI = 48 º.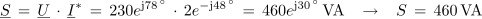
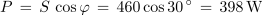
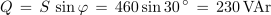
Primer:
2. Izračunaj navidezno delovno in jalovo moč izmeničnega toka v vezavi iz prvega primera tega poglavja (U = 1,2 • ej0º V, I = 0,745 • e-j7,12º A).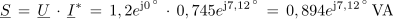
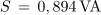
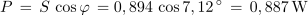
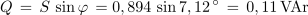
V sestavljenem izmeničnem krogu na splošno velja:
- Kompleksna moč večjega števila porabnikov je enaka vsoti kompleksnih moči posameznih porabnikov ne glede na vezavo le-teh.
| | 5 Realnost izmeničnih krogov |