Iz e-ELEKTROTEHNIKA plus
Zapisali jo bomo v obliki
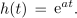
Matematična funkcija zahteva v argumentu neimenovano število, pri času t ima konstanta a enoto s-1. Nekaj podobnega smo zasledili pri argumentu (kotu ωt) harmonične funkcije. Poiščimo odvod eksponentne funkcije[1]:
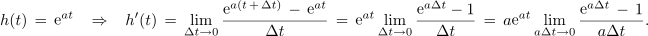
Limitiranje uženemo z vpeljavo spremenljivke s,
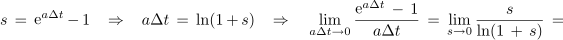
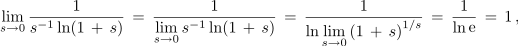
kar končno da:
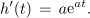
Posebnost eksponentne funkcije je v tem, da se odvod in integral izražata z njo samo:
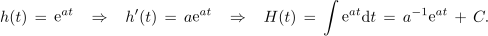
Zgled 4
Polnilni tok kondenzatorja, ki je ob t0 = 0 prazen, je i = 10 mA.e-t / 2 s; Q(t0) = 0 C. Ob t0 = 0 je jakost toka 10 mA, po dveh sekundah 10 mA / e, po štirih 10 mA / e2, po šestih 10 mA / e3, po 10 s pa komaj še 10 mA / e5 ≅ 0,067 mA, kar ustreza komaj 2/3 % začetnega toka. Izračunajmo naboj, ki priteče na ploščo do 10 sekunde. ⇒ Račun je podoben prejšnjemu. Tok je odvod naboja:
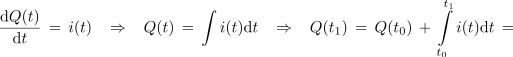
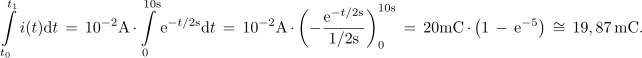
Po zelo (zelo) dolgem času bo naboj dosegel vrednost 20 mC.
Opombe
- ↑ Iz matematike vemo, da je
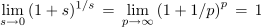
| | 5.8 Polnjenje kondenzatorja |
