Iz e-ELEKTROTEHNIKA plus
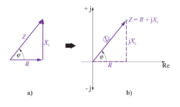
»Prehod« realnih električnih količin v algebrsko kompleksno obliko si oglejmo najprej na preprostih primerih impedance in admitance. Če trikotnik upornosti, npr. izmeničnega kroga z zaporedno vezavo upora in tuljave (sl. 3.4.10 a), prenesemo v kompleksno ravnino tako, kot kaže sl. 3.4.10 b, smo impedanci »nadeli« algebrsko kompleksno obliko.
- Kazalcu impedance Z priredimo v kompleksni ravnini kompleksor (Z), delovni komponenti R pozitivno realno komponento (R) kompleksorja Z ter jalovi induktivni komponenti XL impedance Z pozitivno imaginarno komponento (+ jXL) kompleksorja Z.
Algebrski zapis impedance zaporedne vezave upora in tuljave ima torej v kompleksni ravnini obliko:
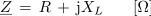
- Impedanca Z je v kompleksni ravnini določena z absolutno vrednostjo |Z| kompleksorja impedance Z.
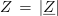
oziroma
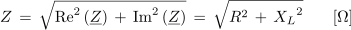
Impedanco izmeničnega kroga z zaporedno vezavo upora z upornostjo 20 Ω in tuljave z induktivno 30 Ω zapišemo potem v kompleksni obliki na način:
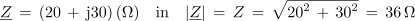
Fazni kot zaporedne vezave izračunamo v kompleksni obliki na osnovi imaginarne in realne komponente kompleksorja impedance ali admitance:
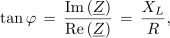
kar je že znana zgodba.
Podobno bi lahko naredili z impedanco kapacitivnega značaja, kompleksor impedance pa bi imel negativno imaginarno komponento (- jXC).
- Induktivna jalova komponenta XL impedance Z ima v kompleksni ravnini značaj pozitivne imaginarne komponente (jXL) kompleksorja Z.
- Kapacitivna jalova komponenta XC impedance Z ima v kompleksni ravnini značaj negativne imaginarne komponente (- jXC) kompleksorja Z.
Algebrski zapis impedance kapacitivnega značaja ima torej v kompleksni ravnini obliko:
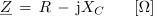
Impedanco izmeničnega kroga z zaporedno vezavo upora z upornostjo 40 Ω in kondenzatorja s kapacitivno upornostjo 50 Ω zapišemo potem v obliki:
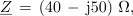
njena absolutna vrednost pa je
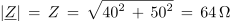
Vidimo, da se zapisa impedanc induktivnega in kapacitivnega značaja v kompleksni obliki razlikujeta v predznakih imaginarnih komponent. Ta ugotovitev je pomembna tudi za določitev značaja impedance ter delovne in jalove upornosti iz rezultata reševanja naloge sestavljene vezave.
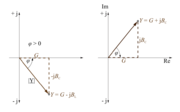
- Pozitivni predznak imaginarne komponente (+ jX) kompleksorja impedance Z določa induktivni značaj impedance Z in pozitivni predznak faznega kota φ.
- Negativni predznak imaginarne komponente (- jX) kompleksorja impedance Z določa kapacitivni značaj impedance Z in negativni predznak faznega kota φ.
Kompleksni obliki zapisov admitanc induktivnega in kapacitivnega značaja dobimo na podoben način na osnovi trikotnikov admitanc (slika 3.4.12):
- Kazalcu admitance Y priredimo v kompleksni ravnini kompleksor Y.
- Delovni komponenti G admitance Y priredimo v kompleksni ravnini pozitivno realno komponento (G), induktivni jalovi komponenti BL negativno imaginarno komponento (- jBL) in kapacitivni jalovi komponenti BC admitance Y pozitivno (+ jBC) kompleksorja Y.
Algebrska zapisa admitanc induktivnega in kapacitivnega značaja imata torej v kompleksni ravnini obliko:
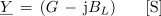
in
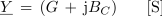
Admitanca Y je v kompleksni ravnini določena z absolutno vrednostjo |Y| kompleksorja admitance Y.
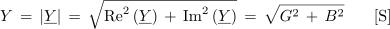
Fazni kot vzporedne vezave izračunamo na osnovi imaginarne in realne komponente na podoben način, kot smo to ugotovili za primer impedance.
Iz slike 3.4.12 in dobljenih izrazov za admitanco Y ugotavljamo, da ima predznak imaginarne komponente kompleksorja admitance nasproten pomen kot predznak imaginarne komponente kompleksorja impedance.
Primer:
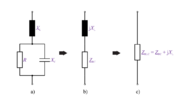
1. Izračunaj impedanco in fazni kot vezave upornosti, ki jo prikazuje slika 3.4.13 a. Upornost upora je 2 Ω, kapacitivna upornost je 4 Ω in induktivna upornost je 1Ω.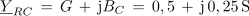
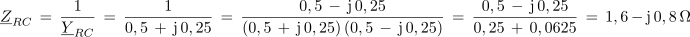
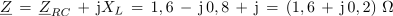
Iz izračunane impedance vezave v kompleksni obliki ugotavljamo: 1. Impedanca ima zaradi pozitivnega predznaka imaginarne komponente, induktivni značaj.2. Upornost delovne komponente impedance je 1,6 Ω, upornost jalove komponente pa 0,2 Ω. 3. Sestavljeno vezavo upornosti na sliki 3.4.13 a. bi lahko glede izvora enakovredno nadomestili z zaporedno vezavo upora z upornostjo 1,6 Ω in tuljave z induktivno upornostjo 0,2 Ω. Impedanca vezave:
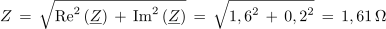
Fazni kot vezave:
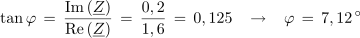
Primer:
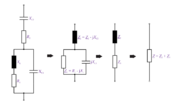
2. Izračunaj impedanco in fazni kot sestavljene vezave upornosti, ki jo prikazuje slika 3.4.14 (R1 = 3 Ω, XL = 4 Ω, XC1 = 4 Ω, R2 = 2 Ω in XC2 = 4 Ω).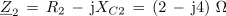
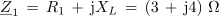
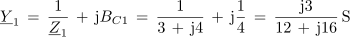
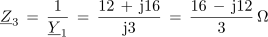
Impedanca celotne vezave v kompleksni obliki je po tem:
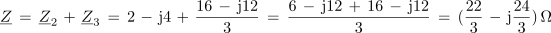
Impedanca vezave ima kapacitivni značaj (- j). Glede obremenitve izvora bi jo lahko nadomestili z zaporedno vezavo upora z upornostjo 22/3 Ω in kondenzatorja s kapacitivno upornostjo 24/3 Ω. Fazni kot vezave:
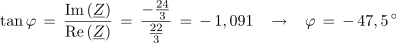
| | 4.1.2.2 Računanje sinusnih napetosti in tokov v eksponentni kompleksni obliki |