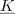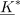1.3.1 Kompleksna količina in kazalec

Iz e-ELEKTROTEHNIKA plus

Redakcija: 16:09, 14. maj 2010 (view source) Admin (Pogovor | prispevki) m (1 revision) ← Starejša redakcija		Trenutna redakcija s časom 16:40, 12. julij 2010 (view source) Admin (Pogovor | prispevki)
(3 intermediate revisions not shown)
Vrstica 1:		Vrstica 1:
-	[[Image:OET2 a poglavje 09 slika 03.svg|thumb|Konjugirani števili <latex>a(\alpha)</latex> in <latex>a(-\alpha)</latex> ležita na enotini krožnici polmera 1.]] [[Image:OET2 a poglavje 09 slika 04.svg|thumb|Konjugirani števili ležita v II. in III. kvadrantu; razlikujeta se le v imaginarnem delu, imata pa enaki absolutni vrednosti.]] Za potrebe analize harmonično vzbujanih vezij vpeljemo določene ''kompleksne količine''«; te so (zgolj in le simbolično) pridružene pravim, električnim količinam: napetosti, toku, moči, ... 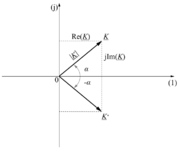Najprej pa izpostavimo določene uveljavljene dogovore!	+	[[Image:eele_slika_visji_013.svg|thumb|Slika 13: Kazalec <latex>{\underline K}</latex>, njegova realni in imaginarni del ter njemu konjugiran kazalec <latex>{\underline K}*</latex>.]]
		+	Za potrebe analize harmonično vzbujanih vezij vpeljemo določene ''kompleksne količine''«; te so (zgolj in le simbolično) pridružene pravim, električnim količinam: napetosti, toku, moči ... Najprej pa izpostavimo določene uveljavljene dogovore.
	Simbol (črko) kompleksne količine podčrtujemo (to naredi razviden razloček med fizikalno in njej prirejeno kompleksno količino). Če je črka <latex>u</latex> simbol za napetost, potem je znak <latex>(\underline U )</latex> simbol za njej pridruženo »kompleksno napetost«, katere realni del je <latex>{\mathop{\rm Re}\nolimits} (\underline U )</latex>, imaginarni del pa je <latex>{\mathop{\rm Im}\nolimits} (\underline U )</latex>. Čeravno je pri tem <latex>(\underline U )</latex> zgolj kompleksno število, izraženo v voltih, ga v kompleksni ravnini zaradi nazornosti upodabljamo z daljico od izhodišča do točke <latex>(\underline U )</latex>, ki jo opremimo še s strelico _ da postane kvazi-vektor; rečemo mu ''kazalec napetosti''.		Simbol (črko) kompleksne količine podčrtujemo (to naredi razviden razloček med fizikalno in njej prirejeno kompleksno količino). Če je črka <latex>u</latex> simbol za napetost, potem je znak <latex>(\underline U )</latex> simbol za njej pridruženo »kompleksno napetost«, katere realni del je <latex>{\mathop{\rm Re}\nolimits} (\underline U )</latex>, imaginarni del pa je <latex>{\mathop{\rm Im}\nolimits} (\underline U )</latex>. Čeravno je pri tem <latex>(\underline U )</latex> zgolj kompleksno število, izraženo v voltih, ga v kompleksni ravnini zaradi nazornosti upodabljamo z daljico od izhodišča do točke <latex>(\underline U )</latex>, ki jo opremimo še s strelico _ da postane kvazi-vektor; rečemo mu ''kazalec napetosti''.
-	Za imaginarno enoto ne uporabljamo črke i (kot je to ustaljeno v matematiki), ampak j; razlog je v tem, da s (sicer ''ležečo'') črko <latex>i</latex> označujemo tudi električni tok. Črka <latex>{\rm i}</latex> bi torej (formalno) nič ne motila; ali pač! Zaradi teh dopolnitev ter zamenjav, in iz razloga, da upodabljamo v Gaussovi ravnini kazalce različnih količin, bomo osi ravnine označevali zgolj z znakoma (1) in (j) (slika 5).<ref>Osi označujemo tudi z Re in Im, ali realna os in imaginarna os; stvar izbire.</ref>	+	Za imaginarno enoto ne uporabljamo črke i (kot je to ustaljeno v matematiki), ampak j; razlog je v tem, da s (sicer ''ležečo'') črko <latex>i</latex> označujemo tudi električni tok. Črka <latex>{\rm i}</latex> bi torej (formalno) nič ne motila; ali pač! Zaradi teh dopolnitev ter zamenjav, in iz razloga, da upodabljamo v Gaussovi ravnini kazalce različnih količin, bomo osi ravnine označevali zgolj z znakoma (1) in (j) (slika 13).<ref>Osi označujemo tudi z Re in Im, ali realna os in imaginarna os; stvar izbire.</ref>
Vrstica 13:		Vrstica 14:
-	Njegova absolutna vrednost (označujemo jo tudi z nepodčrtano črko) je	+	Njegova absolutna vrednost (označujemo jo tudi z nepodčrtano črko) je:

---

Trenutna redakcija s časom 16:40, 12. julij 2010

Za potrebe analize harmonično vzbujanih vezij vpeljemo določene kompleksne količine«; te so (zgolj in le simbolično) pridružene pravim, električnim količinam: napetosti, toku, moči ... Najprej pa izpostavimo določene uveljavljene dogovore.

Simbol (črko) kompleksne količine podčrtujemo (to naredi razviden razloček med fizikalno in njej prirejeno kompleksno količino). Če je črka simbol za napetost, potem je znak simbol za njej pridruženo »kompleksno napetost«, katere realni del je , imaginarni del pa je . Čeravno je pri tem zgolj kompleksno število, izraženo v voltih, ga v kompleksni ravnini zaradi nazornosti upodabljamo z daljico od izhodišča do točke , ki jo opremimo še s strelico _ da postane kvazi-vektor; rečemo mu kazalec napetosti. Za imaginarno enoto ne uporabljamo črke i (kot je to ustaljeno v matematiki), ampak j; razlog je v tem, da s (sicer ležečo) črko označujemo tudi električni tok. Črka bi torej (formalno) nič ne motila; ali pač! Zaradi teh dopolnitev ter zamenjav, in iz razloga, da upodabljamo v Gaussovi ravnini kazalce različnih količin, bomo osi ravnine označevali zgolj z znakoma (1) in (j) (slika 13).^[1]

Dogovore povzemajo zapisi, ki se naslavlajo na nek splošen kazalec :

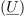
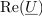
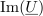
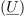
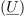
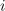
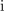
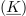
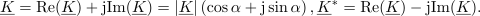
Njegova absolutna vrednost (označujemo jo tudi z nepodčrtano črko) je:

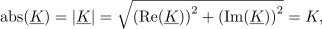
argument pa določa sestavljen izraz:

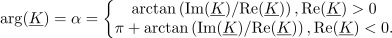
Opombe

1. ↑ Osi označujemo tudi z Re in Im, ali realna os in imaginarna os; stvar izbire.

1.3 Kompleksna števila v kompleksni ravnini

1.3.2 Kazalec harmonične količine