Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (One intermediate revision not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | [[Slika: | + | [[Slika:eele_slika_visji_069.svg|thumb|Slika 69: Raznostraničen trikotnik napetosti razrešuje kosinusni izrek.]] |
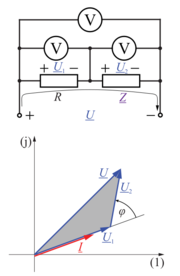
| - | Z napetostno-tokovnim načinom merjenja upornosti merjenca smo se seznanili pri enosmernih vezjih. Če spregledamo popravek merilnega rezultata zaradi izgubnosti merilnikov, potem da kvocient odčitkov voltmetra in ampermetra že kar upornost bremena. Pri merjenju impedance bremena pa | + | Z napetostno-tokovnim načinom merjenja upornosti merjenca smo se seznanili pri enosmernih vezjih. Če spregledamo popravek merilnega rezultata zaradi izgubnosti merilnikov, potem da kvocient odčitkov voltmetra in ampermetra že kar upornost bremena. Pri merjenju impedance bremena pa je drugače, kajti kvocient odčitkov merilnikov bi ustrezal zgolj absolutni vrednosti impedance, nič pa ne bi izvedeli o faznem kotu bremena.<ref>To zmore vektorski merilnik impedance, ki izmeri frekvenčno odvisnost absolutne vrednosti in faznega kota merjenca.</ref> Možen izhod ponuja merjenje efektivnih (temenskih) vrednosti napetosti na napetostnem delilniku, ki ga sestavljata upor znane upornosti <latex>R</latex>, in merjenec, katerega karakter poznamo in mu želimo izmeriti impedanco <latex>\underline Z</latex> (slika 4). Kazalec <latex>\underline U _1</latex> napetosti upora je v fazi s tokom <latex>\underline I</latex>, kazalec <latex>\underline U _2</latex> napetosti merjenca (ako ima ta npr. induktivni karakter) prehiteva tok za fazni kot <latex>\varphi</latex>. Kazalec <latex>\underline U _3</latex> celotne napetosti je paralelogramska vsota prejšnjih dveh.<ref>V primeru merjenca kapacitivnega značaja bi kazalec njegove napetosti kasnil za kazalcem toka; faktor delavnosti bi izračunali po isti formuli, sinus faznega kota pa bi bil negativen.</ref> Pojavi se trikotnik s stranicami <latex>\underline U _1</latex>, <latex>\underline U _2</latex> in <latex>\underline U _3</latex>. Če z voltmetri izmerimo absolutne vrednosti napetosti, se v nadaljevanju opremo le še na kosinusni izrek: |
| Vrstica 22: | Vrstica 22: | ||
| - | S tem načinom smo določili impedanco merjenca le pri določeni vzbujalni frekvenci | + | S tem načinom smo določili impedanco merjenca le pri določeni vzbujalni frekvenci. Če pa bi nas zanimala impedanca merjenca še pri katerih drugih, bi morali ves postopek ponoviti še z vzbujanji s temi drugimi frekvencami.<ref>Temu opravilu rečemo merjenje frekvenčne karakteristike merjenca.</ref> |
| - | '''Zgled 2 | + | '''Zgled 2''' |
| - | Merjenec | + | Merjenec naj bo neznan ''R-C'' dvopol. Določiti mu želimo impedanco pri frekvenci <latex>f</latex>. Delilnik naj oblikujeta merjenc in upor upornosti 30 <latex>\Omega</latex>; vzbuja naj ga vir frekvence <latex>f</latex>. Na uporu izmerimo <latex>|\underline U _1|= 17,5\,{\mathrm{V}}</latex>, na merjencu <latex>|\underline U _2|= 10,8\,{\mathrm{V}}</latex>, na viru pa vrednost <latex>|\underline U _3|= 24\,{\mathrm{V}}</latex>. Izračunajmo sedaj <latex>\underline Z</latex> dvopola. ⇒ Uporabimo formule: |
Trenutna redakcija s časom 18:07, 12. julij 2010
Z napetostno-tokovnim načinom merjenja upornosti merjenca smo se seznanili pri enosmernih vezjih. Če spregledamo popravek merilnega rezultata zaradi izgubnosti merilnikov, potem da kvocient odčitkov voltmetra in ampermetra že kar upornost bremena. Pri merjenju impedance bremena pa je drugače, kajti kvocient odčitkov merilnikov bi ustrezal zgolj absolutni vrednosti impedance, nič pa ne bi izvedeli o faznem kotu bremena.[1] Možen izhod ponuja merjenje efektivnih (temenskih) vrednosti napetosti na napetostnem delilniku, ki ga sestavljata upor znane upornosti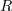
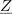
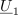
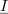
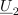
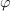
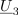
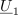
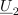
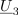
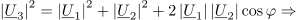
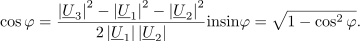
Iz izmerjenih vrednosti sledi faktor delavnosti bremena. Absolutna vrednost impedance bremena je enaka kvocientu absolutne vrednosti napetosti |U2| in absolutne vrednosti toka |I|, ki sledi iz vrednosti |U1| in znane upornosti R:
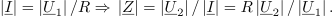
Iz izračunov končno izide impedanca merjenca:
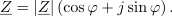
S tem načinom smo določili impedanco merjenca le pri določeni vzbujalni frekvenci. Če pa bi nas zanimala impedanca merjenca še pri katerih drugih, bi morali ves postopek ponoviti še z vzbujanji s temi drugimi frekvencami.[3]
Zgled 2
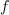
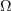
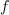
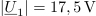
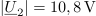
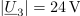
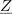
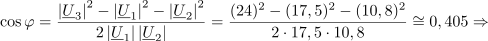
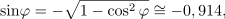
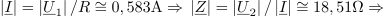
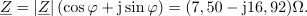
Opombe
- ↑ To zmore vektorski merilnik impedance, ki izmeri frekvenčno odvisnost absolutne vrednosti in faznega kota merjenca.
- ↑ V primeru merjenca kapacitivnega značaja bi kazalec njegove napetosti kasnil za kazalcem toka; faktor delavnosti bi izračunali po isti formuli, sinus faznega kota pa bi bil negativen.
- ↑ Temu opravilu rečemo merjenje frekvenčne karakteristike merjenca.
| | 3.3 R-C delilnik |