Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
| (2 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
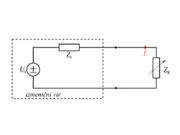
| - | [[Slika: | + | [[Slika:eele_slika_visji_048.svg|thumb|Slika 48: Breme spremenljive impedance je priključeno na realen izmenični vir; sprašujemo se po primerni vrednosti impedance bremena, da bo delovna moč v njem največja.]] |
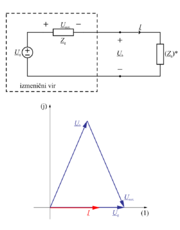
| - | [[Slika: | + | [[Slika:eele_slika_visji_049.svg|thumb|Slika 49: Kazalčni diagram toka in napetosti v primeru, ko je na izmenični vir priključeno prilagojeno breme. ]] |
| - | Pojem prilagoditve smo obdelali že pri enosmernih vezjih, ob vprašanju | + | Pojem prilagoditve smo obdelali že pri enosmernih vezjih, ob vprašanju, kolikšna naj bo upornost bremena, ki ga priključimo na realen vir, da bo moč v bremenu maksimalna. Ugotovili smo, da je tolikšna takrat, ko je upornost bremena enaka nadomestni notranji upornosti vira. |
| - | In kako je s to rečjo v izmeničnem vezju? Imejmo nek realen harmonični vir z določeno nadomestno notranjo impedanco. Modelno vezje takšnega vira oblikuje npr. zaporedna vezava neodvisnega napetostnega vira, ki mu pripada kazalec <latex>\underline U_{\mathrm{g}}</latex>, in pasivnega dvopola, katerega impedanca <latex>\underline Z_{\mathrm{g}}</latex> ustreza nadomestni notranji impedanci vira. Na vir priključimo kompleksno breme (slika | + | In kako je s to rečjo v izmeničnem vezju? Imejmo nek realen harmonični vir z določeno nadomestno notranjo impedanco. Modelno vezje takšnega vira oblikuje npr. zaporedna vezava neodvisnega napetostnega vira, ki mu pripada kazalec <latex>\underline U_{\mathrm{g}}</latex>, in pasivnega dvopola, katerega impedanca <latex>\underline Z_{\mathrm{g}}</latex> ustreza nadomestni notranji impedanci vira. Na vir priključimo kompleksno breme (slika 48) in se vprašajmo, kolikšna naj bo impedanca <latex>\underline Z_{\mathrm{b}}</latex> bremena, da bo delovna moč <latex>P_{\mathrm{b}}</latex> v njem maksimalna. Aktivna moč je določena z realnim delom kazalca moči: |
| Vrstica 22: | Vrstica 22: | ||
| - | Izraz spominja na enosmerno vezje | + | Izraz spominja na enosmerno vezje, kot da bi na enosmerni vir z napetostjo odprtih sponk; <latex>U_{\mathrm{g\,ef.}}</latex> in notranjo upornostjo <latex>R_{\mathrm{g}}</latex> priključili breme z upornostjo <latex>R_{\mathrm{b}}</latex> in se vprašali po moči v bremenu. Ker pa odgovor od tam že poznamo (da je moč v bremenu maksimalna, ko je njegova upornost enaka notranji), sledi: Aktivna moč v kompleksnem bremenu je maksimalna takrat, ko je rezistanca bremena enaka rezistanci notranjega elementa in ko je hkrati tudi reaktanca bremena enaka negativni reaktanci notranjega elementa: |
| Vrstica 28: | Vrstica 28: | ||
| - | Odgovor je tu | + | Odgovor je tu. Delovna moč v kompleksnem bremenu je maksimalna takrat, ko je impedanca bremena enaka konjugirani notranji impedanci vira. Takrat pravimo, da je kompleksno breme ''prilagojeno'' na realen harmonični vir. |
| Vrstica 43: | Vrstica 43: | ||
| - | Ob prilagoditvi oblikujeta kazalca delnih napetosti s kazalcem napetosti vira enakokrak trikotnik, preseneča pa to, da sta v primeru <latex>X_{\mathrm{g}} \gg R_{\mathrm{g}}</latex> kraka tega trikotnika zelo dolga, da je absolutna vrednost kazalca napetosti na bremenu takrat celo nekajkrat večja od absolutne vrednosti kazalca napetosti odprtih sponk; spet nekaj, česar v enosmernih razmerah nismo srečali (slika | + | Ob prilagoditvi oblikujeta kazalca delnih napetosti s kazalcem napetosti vira enakokrak trikotnik, preseneča pa to, da sta v primeru <latex>X_{\mathrm{g}} \gg R_{\mathrm{g}}</latex> kraka tega trikotnika zelo dolga, da je absolutna vrednost kazalca napetosti na bremenu takrat celo nekajkrat večja od absolutne vrednosti kazalca napetosti odprtih sponk; spet nekaj, česar v enosmernih razmerah nismo srečali (slika 49). |
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 18:28, 12. julij 2010
Pojem prilagoditve smo obdelali že pri enosmernih vezjih, ob vprašanju, kolikšna naj bo upornost bremena, ki ga priključimo na realen vir, da bo moč v bremenu maksimalna. Ugotovili smo, da je tolikšna takrat, ko je upornost bremena enaka nadomestni notranji upornosti vira.
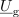
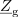
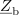
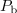
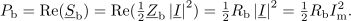
Amplitudo toka določa kvocient amplitude napetosti neodvisnega vira in absolutne vrednosti vsote notranje impedance in impedance bremena:
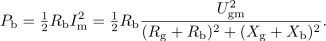
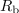
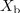
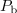
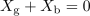
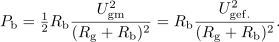
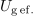
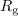
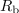
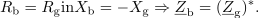
Odgovor je tu. Delovna moč v kompleksnem bremenu je maksimalna takrat, ko je impedanca bremena enaka konjugirani notranji impedanci vira. Takrat pravimo, da je kompleksno breme prilagojeno na realen harmonični vir.
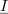
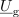
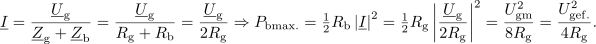
Zanimiva sta tudi kazalca napetosti na notranjem elementu in na bremenu:
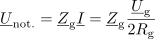
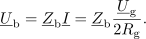
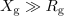
| | 3.6 Tokovni generator |