Iz e-ELEKTROTEHNIKA plus
| Vrstica 1: | Vrstica 1: | ||
| - | Ta vezava se najpogosteje uporablja pri simetričnih bremenih, so pa tudi izjeme. Bistvo trikotne vezave je v tem, da je vsako breme priključeno na svojo medfazno napetost (slika | + | [[Slika:eele_slika_visji_088.svg|thumb|Slika 88: Trifazno breme v trikotni vezavi.]] |
| + | [[Slika:eele_slika_visji_089.svg|thumb|Slika 89: RLC trifazno breme breme v trikotni vezavi.]] | ||
| + | [[Slika:eele_slika_visji_090.svg|thumb|Slika 90: Kazalčni diagram tokov skozi bremena in linijskih tokov v primeru simetričnega trifaznega bremena v trikotni vezavi. Risanje kazalcev faznih in medfaznih napetosti smo zaradi predglednosti opustili.]] | ||
| + | |||
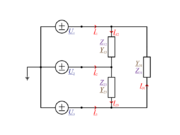
| + | Ta vezava se najpogosteje uporablja pri simetričnih bremenih, so pa tudi izjeme. Bistvo trikotne vezave je v tem, da je vsako breme priključeno na svojo medfazno napetost (slika 88). Breme z admitanco <u>''Y''</u><sub>12</sub> je na napetosti, ki jo določa kazalec <u>''U''</u><sub>12</sub>, podobno tudi drugi dve bremeni. Kazalci tokov skozi bremena so: | ||
| + | |||
<latex>{{{\underline I }_{12}}\, =\, {{\underline Y }_{12}}{{\underline U }_{12}}\,\,,\,\,\,\,{\rm{ }}{{\underline I }_{23}}\, =\, {{\underline Y }_{23}}{{\underline U }_{23}}\,\,\,\,{\rm{ in }}\,\,\,\,{{\underline I }_{31}} \,=\,{{\underline Y }_{31}}{{\underline U }_{31}},}</latex> | <latex>{{{\underline I }_{12}}\, =\, {{\underline Y }_{12}}{{\underline U }_{12}}\,\,,\,\,\,\,{\rm{ }}{{\underline I }_{23}}\, =\, {{\underline Y }_{23}}{{\underline U }_{23}}\,\,\,\,{\rm{ in }}\,\,\,\,{{\underline I }_{31}} \,=\,{{\underline Y }_{31}}{{\underline U }_{31}},}</latex> | ||
| + | |||
toke faznih vodnikov pa dobimo iz spojiščnih enačb: | toke faznih vodnikov pa dobimo iz spojiščnih enačb: | ||
| + | |||
<latex>{{{\underline I }_1}\, =\, {{\underline I }_{12}}\, -\, {{\underline I }_{31}}\,\,,\,\,\,\,{\rm{ }}{{\underline I}_2}\, =\, {{\underline I }_{23}}\, - \,{{\underline I }_{12}}\,\,\,\,{\rm{ in }}\,\,\,\,{{\underline I }_3} \,=\, {{\underline I }_{31}}\, -\, {{\underline I }_{23}}.}</latex> | <latex>{{{\underline I }_1}\, =\, {{\underline I }_{12}}\, -\, {{\underline I }_{31}}\,\,,\,\,\,\,{\rm{ }}{{\underline I}_2}\, =\, {{\underline I }_{23}}\, - \,{{\underline I }_{12}}\,\,\,\,{\rm{ in }}\,\,\,\,{{\underline I }_3} \,=\, {{\underline I }_{31}}\, -\, {{\underline I }_{23}}.}</latex> | ||
| + | |||
'''Zgled 2''' | '''Zgled 2''' | ||
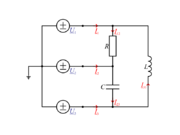
| - | Izberimo trikotno vezje upora prevodnosti ''G'', ki je priključen na prvo, kondenzatorja admitance j''G'' / √3, ki je priključen na drugo, in tuljave z admitanco -j''G'' / √3, ki je priključena na zadnjo medfazno napetost (slika | + | Izberimo trikotno vezje upora prevodnosti ''G'', ki je priključen na prvo, kondenzatorja admitance j''G'' / √3, ki je priključen na drugo, in tuljave z admitanco -j''G'' / √3, ki je priključena na zadnjo medfazno napetost (slika 89). Izračunajmo fazne toke. ⇒ Iz predhodnega razdelka prepišemo kazalce medfaznih napetosti in izračunamo najprej kazalce tokov skozi bremena: |
| + | |||
<latex>{\underline U _{12}}\, =\, 0,5 \,\cdot\, \left( { - 1 \,+\, {\rm{j}}\sqrt 3 } \right)\sqrt 3 {U_{\rm{f}}}\,\,\,\,{\rm{ }} \Rightarrow \,\,\,\,{\rm{ }}{\underline I _{12}} \,= \,G{\underline U _{12}}\, =\, 0,5\, \cdot\, \left( { - \sqrt 3\, + \,{\rm{j}}3} \right)G{U_{\rm{f}}},</latex> | <latex>{\underline U _{12}}\, =\, 0,5 \,\cdot\, \left( { - 1 \,+\, {\rm{j}}\sqrt 3 } \right)\sqrt 3 {U_{\rm{f}}}\,\,\,\,{\rm{ }} \Rightarrow \,\,\,\,{\rm{ }}{\underline I _{12}} \,= \,G{\underline U _{12}}\, =\, 0,5\, \cdot\, \left( { - \sqrt 3\, + \,{\rm{j}}3} \right)G{U_{\rm{f}}},</latex> | ||
| + | |||
<latex>{\underline U _{23}}\, =\, \sqrt 3 {U_{\rm{f}}}\,\,\,\,{\rm{ }} \Rightarrow \,\,\,\,{\rm{ }}{\underline I _{23}}\, =\, \left( {{\rm{j}}G/\sqrt 3 } \right){\underline U _{23}}\, = \,{\rm{j}}G{U_{\rm{f}}},</latex> | <latex>{\underline U _{23}}\, =\, \sqrt 3 {U_{\rm{f}}}\,\,\,\,{\rm{ }} \Rightarrow \,\,\,\,{\rm{ }}{\underline I _{23}}\, =\, \left( {{\rm{j}}G/\sqrt 3 } \right){\underline U _{23}}\, = \,{\rm{j}}G{U_{\rm{f}}},</latex> | ||
| + | |||
<latex>{\underline U _{31}}\, = \,0,5 \,\cdot \,\left( { - 1\, -\, {\rm{j}}\sqrt 3 } \right)\sqrt 3 {U_{\rm{f}}}\,\,\,\,{\rm{ }} \Rightarrow\,\,\,\, {\rm{ }}{\underline I _{31}} \,= \,\left( { -{\rm{j}}G/\sqrt 3 } \right){\underline U _{31}} \,= \,0,5 \,\cdot \,\left( { - \sqrt 3 \, + \,{\rm{j}}} \right)G{U_{\rm{f}}}.{\rm{ }}</latex> | <latex>{\underline U _{31}}\, = \,0,5 \,\cdot \,\left( { - 1\, -\, {\rm{j}}\sqrt 3 } \right)\sqrt 3 {U_{\rm{f}}}\,\,\,\,{\rm{ }} \Rightarrow\,\,\,\, {\rm{ }}{\underline I _{31}} \,= \,\left( { -{\rm{j}}G/\sqrt 3 } \right){\underline U _{31}} \,= \,0,5 \,\cdot \,\left( { - \sqrt 3 \, + \,{\rm{j}}} \right)G{U_{\rm{f}}}.{\rm{ }}</latex> | ||
| + | |||
V naslednjem koraku izračunamo še linijske toke: | V naslednjem koraku izračunamo še linijske toke: | ||
| + | |||
<latex>{\underline I _1}\, = \,{\underline I _{12}}\, -\, {\underline I _{31}}\, = \,0,5\, \cdot \,\left( { - \sqrt 3\, + \,{\rm{j}}3} \right)G{U_{\rm{f}}} \,- \,0,5 \,\cdot \,\left( { - \sqrt 3 \,+ \,{\rm{j}}} \right)G{U_{\rm{f}}}\, = \,{\rm{j}}G{U_{\rm{f}}} \,= \,G{\underline U _1},</latex> | <latex>{\underline I _1}\, = \,{\underline I _{12}}\, -\, {\underline I _{31}}\, = \,0,5\, \cdot \,\left( { - \sqrt 3\, + \,{\rm{j}}3} \right)G{U_{\rm{f}}} \,- \,0,5 \,\cdot \,\left( { - \sqrt 3 \,+ \,{\rm{j}}} \right)G{U_{\rm{f}}}\, = \,{\rm{j}}G{U_{\rm{f}}} \,= \,G{\underline U _1},</latex> | ||
| + | |||
<latex>{\underline I _2}\, =\, {\underline I _{23}} \,-\, {\underline I _{12}}\, = \,{\rm{j}}G{U_{\rm{f}}}\, - \,0,5\, \cdot\, \left( { - \sqrt 3\, + \,{\rm{j}}3} \right)G{U_{\rm{f}}} \,=\, 0,5 \,\cdot\, \left( {\sqrt 3 \, -\, {\rm{j}}} \right)G{U_{\rm{f}}}\, =\, G{\underline U _2},</latex> | <latex>{\underline I _2}\, =\, {\underline I _{23}} \,-\, {\underline I _{12}}\, = \,{\rm{j}}G{U_{\rm{f}}}\, - \,0,5\, \cdot\, \left( { - \sqrt 3\, + \,{\rm{j}}3} \right)G{U_{\rm{f}}} \,=\, 0,5 \,\cdot\, \left( {\sqrt 3 \, -\, {\rm{j}}} \right)G{U_{\rm{f}}}\, =\, G{\underline U _2},</latex> | ||
| + | |||
<latex>{\underline I _3}\, = \,{\underline I _{31}}\, - \,{\underline I _{23}} \,= \,0,5 \,\cdot \,\left( { - \sqrt 3 \, +\, {\rm{j}}} \right)G{U_{\rm{f}}}\, - \,{\rm{j}}G{U_{\rm{f}}} \,= \,0,5 \,\cdot \,\left( { - \sqrt 3 \, - \,{\rm{j}}} \right)G{U_{\rm{f}}}\, =\, G{\underline U _3}.</latex> | <latex>{\underline I _3}\, = \,{\underline I _{31}}\, - \,{\underline I _{23}} \,= \,0,5 \,\cdot \,\left( { - \sqrt 3 \, +\, {\rm{j}}} \right)G{U_{\rm{f}}}\, - \,{\rm{j}}G{U_{\rm{f}}} \,= \,0,5 \,\cdot \,\left( { - \sqrt 3 \, - \,{\rm{j}}} \right)G{U_{\rm{f}}}\, =\, G{\underline U _3}.</latex> | ||
| + | |||
In kaj smo dobili? Dobili smo simetrične kazalce faznih tokov, ki so paroma v fazi s faznimi napetostmi. Čeravno je breme nesimetrično, ga je z vidika virov razumeti kot simetrično uporovno breme. To vezavo uporabljajo pri energijskem napajanju uporovnega dvopola velike moči. Takšnega sicer ne smemo priključiti na omrežje, lahko pa to storimo s pomočjo dodatnih reaktivnih elementov v trikotni vezavi<ref>Primer takšnega bremena je indukcijska lončna peč, ki služi taljenju oziroma pridobivanju legur. Moči indukcijskih peči so lahko velike in sežejo tudi v razred MW.</ref>. | In kaj smo dobili? Dobili smo simetrične kazalce faznih tokov, ki so paroma v fazi s faznimi napetostmi. Čeravno je breme nesimetrično, ga je z vidika virov razumeti kot simetrično uporovno breme. To vezavo uporabljajo pri energijskem napajanju uporovnega dvopola velike moči. Takšnega sicer ne smemo priključiti na omrežje, lahko pa to storimo s pomočjo dodatnih reaktivnih elementov v trikotni vezavi<ref>Primer takšnega bremena je indukcijska lončna peč, ki služi taljenju oziroma pridobivanju legur. Moči indukcijskih peči so lahko velike in sežejo tudi v razred MW.</ref>. | ||
| + | |||
Kazalec moči trojice bremen v trikotni vezavi je enak vsoti kazalcev moči posameznih bremen: | Kazalec moči trojice bremen v trikotni vezavi je enak vsoti kazalcev moči posameznih bremen: | ||
| + | |||
<latex>\underline S \, = \,{\underline S _{12}}\, +\, {\underline S _{23}}\, + \,{\underline S _{31}}\, =\, {\underline U _{12}}({\underline I _{12}})^*\, +\, {\underline U _{23}}({\underline I _{23}})^*\, +\, {\underline U _{31}}({\underline I _{31}})^* = </latex> | <latex>\underline S \, = \,{\underline S _{12}}\, +\, {\underline S _{23}}\, + \,{\underline S _{31}}\, =\, {\underline U _{12}}({\underline I _{12}})^*\, +\, {\underline U _{23}}({\underline I _{23}})^*\, +\, {\underline U _{31}}({\underline I _{31}})^* = </latex> | ||
| + | |||
<latex>({\underline U _1}\, -\, {\underline U _2})({\underline I _{12}})^* \,+ \,({\underline U _2}\, -\, {\underline U _3})({\underline I _{23}})^*\, +\, ({\underline U _3}\, -\, {\underline U _{21}})({\underline I _{31}})^*\, = </latex> | <latex>({\underline U _1}\, -\, {\underline U _2})({\underline I _{12}})^* \,+ \,({\underline U _2}\, -\, {\underline U _3})({\underline I _{23}})^*\, +\, ({\underline U _3}\, -\, {\underline U _{21}})({\underline I _{31}})^*\, = </latex> | ||
| + | |||
<latex>{\underline U _1}(({\underline I _{12}})^*\, -\, ({\underline I _{31}})^*)\, +\, {\underline U _2}(({\underline I _{23}})^*\, -\, ({\underline I _{12}})^*)\, +\, {\underline U _3}(({\underline I _{31}})^*\, -\, ({\underline I _{23}})^*)\,= </latex> | <latex>{\underline U _1}(({\underline I _{12}})^*\, -\, ({\underline I _{31}})^*)\, +\, {\underline U _2}(({\underline I _{23}})^*\, -\, ({\underline I _{12}})^*)\, +\, {\underline U _3}(({\underline I _{31}})^*\, -\, ({\underline I _{23}})^*)\,= </latex> | ||
| + | |||
<latex>{\underline U _1}({\underline I _1})^* \,+ \,{\underline U _2}({\underline I _2})^* \,+\, {\underline U _3}({\underline I _3})^*.</latex> | <latex>{\underline U _1}({\underline I _1})^* \,+ \,{\underline U _2}({\underline I _2})^* \,+\, {\underline U _3}({\underline I _3})^*.</latex> | ||
| Vrstica 38: | Vrstica 59: | ||
Sklep je: | Sklep je: | ||
| + | |||
<latex>{\underline S \, = \,{{\underline U }_1}({{\underline I }_1})^*\, +\, {{\underline U }_2}({{\underline I }_2})^*\, +\, {{\underline U }_3}({{\underline I }_3})^*.}</latex> | <latex>{\underline S \, = \,{{\underline U }_1}({{\underline I }_1})^*\, +\, {{\underline U }_2}({{\underline I }_2})^*\, +\, {{\underline U }_3}({{\underline I }_3})^*.}</latex> | ||
| + | |||
Naj bo trifazno breme v zvezdni ali v trikotni vezavi, izraz za kazalec moči je vsakokrat enak; desna stran ustreza v resnici vsoti kazalcev moči virov. | Naj bo trifazno breme v zvezdni ali v trikotni vezavi, izraz za kazalec moči je vsakokrat enak; desna stran ustreza v resnici vsoti kazalcev moči virov. | ||
| - | Kadar je trifazno breme simetrično, so simetrični tako kazalci bremenskih kot tudi kazalci linijskih tokov (slika | + | |
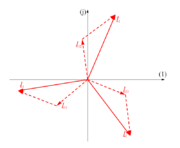
| + | Kadar je trifazno breme simetrično, so simetrični tako kazalci bremenskih kot tudi kazalci linijskih tokov (slika 90). Tipičen primer simetričnega bremena je trifazni motor. Kazalec moči simetričnega bremena je še bolj preprost, saj je kratkomalo trikratnik kazalca moči enega vira: | ||
| + | |||
<latex>{\underline S\, =\, P\, +\, {\rm{j}}Q \,= \,3{U_{\rm{f}}}{I_{\rm{f}}}\left( {\cos \varphi \, +\, {\rm{j}}\sin \varphi } \right)\, =\, \sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\cos \varphi \, +\, {\rm{j}}\sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\sin \varphi .}</latex> | <latex>{\underline S\, =\, P\, +\, {\rm{j}}Q \,= \,3{U_{\rm{f}}}{I_{\rm{f}}}\left( {\cos \varphi \, +\, {\rm{j}}\sin \varphi } \right)\, =\, \sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\cos \varphi \, +\, {\rm{j}}\sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\sin \varphi .}</latex> | ||
| + | |||
'''Zgled 3''' | '''Zgled 3''' | ||
Trifazni asinhronski motor ima nazivno moč 7,5 kW, izkoristek 0,85, faktor moči 0,8 in je priključen na omrežje 3 x 400 V / 230 V, 50 Hz. Izračunajmo efektivno vrednost linijskih tokov in vrednost kapacitivnosti kompenzacijskih kondenzatorjev. ⇒ Izhajamo iz enačbe za moč: | Trifazni asinhronski motor ima nazivno moč 7,5 kW, izkoristek 0,85, faktor moči 0,8 in je priključen na omrežje 3 x 400 V / 230 V, 50 Hz. Izračunajmo efektivno vrednost linijskih tokov in vrednost kapacitivnosti kompenzacijskih kondenzatorjev. ⇒ Izhajamo iz enačbe za moč: | ||
| + | |||
<latex>P \,=\, \sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\cos \varphi \,\,\,\,{\rm{ }} \Rightarrow\,\,\,\, {\rm{ }}{I_{\rm{f}}}\, = \,\frac{P}{{\sqrt 3 {U_{{\rm{m - f}}}}\cos \varphi }} \,=\, \frac{{7500{\rm{ W }}/0,85}}{{\sqrt 3 \,\cdot \,400{\rm{ V}} \,\cdot \,0,8}}\, \cong \,15,9{\rm{ A}}{\rm{.}}</latex> | <latex>P \,=\, \sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\cos \varphi \,\,\,\,{\rm{ }} \Rightarrow\,\,\,\, {\rm{ }}{I_{\rm{f}}}\, = \,\frac{P}{{\sqrt 3 {U_{{\rm{m - f}}}}\cos \varphi }} \,=\, \frac{{7500{\rm{ W }}/0,85}}{{\sqrt 3 \,\cdot \,400{\rm{ V}} \,\cdot \,0,8}}\, \cong \,15,9{\rm{ A}}{\rm{.}}</latex> | ||
| + | |||
Jalova moč je: | Jalova moč je: | ||
| + | |||
<latex>Q \,=\, \sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\sin \varphi \, =\, \sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\sqrt {1\, - \,{{\cos }^2}\varphi }\, \cong\, 6,61{\rm{ kVAr}}{\rm{. }}</latex> | <latex>Q \,=\, \sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\sin \varphi \, =\, \sqrt 3 {U_{{\rm{m - f}}}}{I_{\rm{f}}}\sqrt {1\, - \,{{\cos }^2}\varphi }\, \cong\, 6,61{\rm{ kVAr}}{\rm{. }}</latex> | ||
| + | |||
Jalovo moč kompenzirajo trije kondenzatorji v vezavi trikot, in sicer tako, da vsak od njih kompenzira eno tretjino. Formulo si izposojamo iz prejšnjega poglavja: | Jalovo moč kompenzirajo trije kondenzatorji v vezavi trikot, in sicer tako, da vsak od njih kompenzira eno tretjino. Formulo si izposojamo iz prejšnjega poglavja: | ||
| + | |||
<latex>C \,=\, \frac{Q/3}{{\omega U_{{\rm{m - f}}}^{\rm{2}}}}\, \cong \,\frac{{6610{\rm{ VAr}}/{\rm{3}}}}{{{\rm{100}}\pi {\rm{ }}{{\rm{s}}^{ - 1}} \,\cdot\,{{(400{\rm{ V}})}^2}}} \,\cong \,43,8{\rm{ \mu F}}.</latex> | <latex>C \,=\, \frac{Q/3}{{\omega U_{{\rm{m - f}}}^{\rm{2}}}}\, \cong \,\frac{{6610{\rm{ VAr}}/{\rm{3}}}}{{{\rm{100}}\pi {\rm{ }}{{\rm{s}}^{ - 1}} \,\cdot\,{{(400{\rm{ V}})}^2}}} \,\cong \,43,8{\rm{ \mu F}}.</latex> | ||
| + | |||
Lahko pa kompenzacijske kondenzatorje vežemo tudi v zvezdo, vendar so takrat njihove vrednosti trikratne, saj je efektivna napetost na njih le 230 V. | Lahko pa kompenzacijske kondenzatorje vežemo tudi v zvezdo, vendar so takrat njihove vrednosti trikratne, saj je efektivna napetost na njih le 230 V. | ||
Trenutna redakcija s časom 13:09, 15. avgust 2010
Ta vezava se najpogosteje uporablja pri simetričnih bremenih, so pa tudi izjeme. Bistvo trikotne vezave je v tem, da je vsako breme priključeno na svojo medfazno napetost (slika 88). Breme z admitanco Y12 je na napetosti, ki jo določa kazalec U12, podobno tudi drugi dve bremeni. Kazalci tokov skozi bremena so:
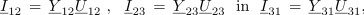
toke faznih vodnikov pa dobimo iz spojiščnih enačb:
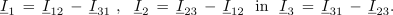
Zgled 2
Izberimo trikotno vezje upora prevodnosti G, ki je priključen na prvo, kondenzatorja admitance jG / √3, ki je priključen na drugo, in tuljave z admitanco -jG / √3, ki je priključena na zadnjo medfazno napetost (slika 89). Izračunajmo fazne toke. ⇒ Iz predhodnega razdelka prepišemo kazalce medfaznih napetosti in izračunamo najprej kazalce tokov skozi bremena:
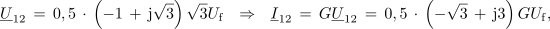
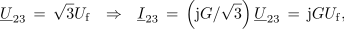

V naslednjem koraku izračunamo še linijske toke:
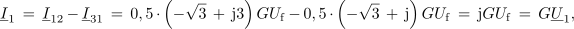
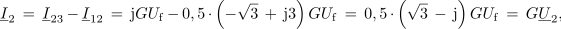
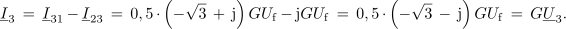
In kaj smo dobili? Dobili smo simetrične kazalce faznih tokov, ki so paroma v fazi s faznimi napetostmi. Čeravno je breme nesimetrično, ga je z vidika virov razumeti kot simetrično uporovno breme. To vezavo uporabljajo pri energijskem napajanju uporovnega dvopola velike moči. Takšnega sicer ne smemo priključiti na omrežje, lahko pa to storimo s pomočjo dodatnih reaktivnih elementov v trikotni vezavi[1].
Kazalec moči trojice bremen v trikotni vezavi je enak vsoti kazalcev moči posameznih bremen:
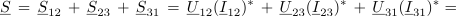
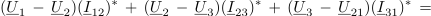

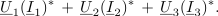
Sklep je:
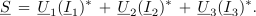
Naj bo trifazno breme v zvezdni ali v trikotni vezavi, izraz za kazalec moči je vsakokrat enak; desna stran ustreza v resnici vsoti kazalcev moči virov.
Kadar je trifazno breme simetrično, so simetrični tako kazalci bremenskih kot tudi kazalci linijskih tokov (slika 90). Tipičen primer simetričnega bremena je trifazni motor. Kazalec moči simetričnega bremena je še bolj preprost, saj je kratkomalo trikratnik kazalca moči enega vira:
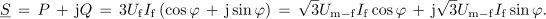
Zgled 3
Trifazni asinhronski motor ima nazivno moč 7,5 kW, izkoristek 0,85, faktor moči 0,8 in je priključen na omrežje 3 x 400 V / 230 V, 50 Hz. Izračunajmo efektivno vrednost linijskih tokov in vrednost kapacitivnosti kompenzacijskih kondenzatorjev. ⇒ Izhajamo iz enačbe za moč:
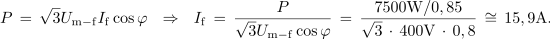
Jalova moč je:
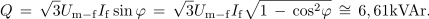
Jalovo moč kompenzirajo trije kondenzatorji v vezavi trikot, in sicer tako, da vsak od njih kompenzira eno tretjino. Formulo si izposojamo iz prejšnjega poglavja:
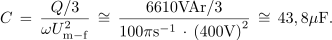
Lahko pa kompenzacijske kondenzatorje vežemo tudi v zvezdo, vendar so takrat njihove vrednosti trikratne, saj je efektivna napetost na njih le 230 V.
Opombe
- ↑ Primer takšnega bremena je indukcijska lončna peč, ki služi taljenju oziroma pridobivanju legur. Moči indukcijskih peči so lahko velike in sežejo tudi v razred MW.
| | 7.6 Trifazni prenos energije in trifazna transformacija |