Iz e-ELEKTROTEHNIKA plus
m (1 revision) |
|||
| (3 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
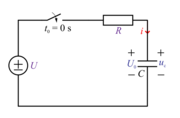
| - | Z omenjenim vezjem | + | [[Slika:eele_slika_visji_097.svg|thumb|Slika 97: Polnilno vezje že delno naelektrenega kondenzatorja.]] |
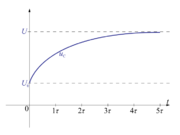
| + | [[Slika:eele_slika_visji_098.svg|thumb|Slika 98: Diagram spreminjanja napetosti na kondenzatorju od začetne do končne vrednosti.]] | ||
| + | Z omenjenim vezjem lahko polnimo tudi že predhodno delno naelektren kondenzator (slika 97), njegova prednapetost naj bo ''U''<sub>0</sub>. Ob vklopu, ''t''<sub>0</sub> = 0 s, bo vrednost toka največja (določata jo razlika napetosti vira ''U'' in prednapetosti ''U''<sub>0</sub> in upornost upora). V nadaljevanju bo tok plahnel po prej ugotovljeni eksponentni odvisnosti, | ||
| + | |||
<latex>{i\, =\, \frac{U \,-\, {U_0}}{R}{{\mathop{\rm e}\nolimits} ^{ - t/\tau }},}</latex> | <latex>{i\, =\, \frac{U \,-\, {U_0}}{R}{{\mathop{\rm e}\nolimits} ^{ - t/\tau }},}</latex> | ||
| - | |||
| - | < | + | napetost ''u<sub>C</sub>'' pa bo od začetne ''U''<sub>0</sub> rasla in se bližala vrednosti ''U'' (slika 98)<ref>Rešitev je takšna, kot da bi v prejšnjih časovnih diagramih ordinatno os premaknili za čas, kateremu ustreza začetna vrednost polnilnega toka.</ref>: |
| - | |||
| - | |||
| - | <latex>{u_C} | + | <latex>{{u_C}\, =\, {U_0}\, +\, (U \,- \,{U_0})\left( {1\, -\, {{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right).}</latex> |
| - | |||
| - | + | '''Zgled 2''' | |
| - | + | Kondenzator najprej naelektrimo na polno napetost z virom napetosti ''U'' ter stikalo izključimo, nato kondenzator odklopimo in ga v obratni polariteti spet priklopimo v vezje. Njegova prednapetost ''U''<sub>0</sub> je tedaj ravno -''U''. Zatem stikalo spet vključimo. Določimo čas t*, ob katerem bo napetost kondenzatorja enaka 0 V. ⇒ Prejšnjo enačbo zapišemo za trenutek ''t''<sup>*</sup> ter ga iz nje izračunamo: | |
| - | + | ||
| + | <latex>{u_C}(t) \,=\, {U_0}\, +\, (U \,-\, {U_0})\left( {1\, -\, {{\mathop{\rm e}\nolimits} ^{ - t/\tau }}} \right){\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{u_C}({t^*})\, = \, -\, U\, +\, (U\, +\, U))\left( {1 - {{\mathop{\rm e}\nolimits} ^{ - {t^*}/\tau }}} \right) = 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, </latex> | ||
| + | <latex>1 \,- \,{{\mathop{\rm e}\nolimits} ^{ - {t^*}/\tau }} \,=\, 1/2{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{{\mathop{\rm e}\nolimits} ^{{t^*}/\tau }}\, = \,2{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{t^*}/\tau\, = \,\ln 2{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{t^*} \,= \,\tau \ln 2 \,\cong\, 0,693\, \cdot\, \tau .</latex> | ||
| + | V času 69 % časovne konstante bo napetost na kondenzatorju ravno nič voltov, takoj zatem pa se bo pričela vzpenjati k vrednosti ''U''. | ||
| + | V preteklih primerih smo napetostni vir smatrali za idealen, da ima notranjo upornost enako nič. Brž ko bi ne bil takšen, bi se njegova notranja upornost ''R''<sub>not</sub>. pridružila upornosti polnilnega predupora. Časovna konstanta ''τ'' bi bila takrat nekoliko daljša, ''τ'' = (''R''<sub>not</sub> + ''R'')''C'', enako tudi proces polnjenja, končna napetost kondenzatorja pa bi bila enaka napetosti odprtih sponk vira. | ||
Trenutna redakcija s časom 14:01, 15. avgust 2010
Z omenjenim vezjem lahko polnimo tudi že predhodno delno naelektren kondenzator (slika 97), njegova prednapetost naj bo U0. Ob vklopu, t0 = 0 s, bo vrednost toka največja (določata jo razlika napetosti vira U in prednapetosti U0 in upornost upora). V nadaljevanju bo tok plahnel po prej ugotovljeni eksponentni odvisnosti,
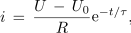
napetost uC pa bo od začetne U0 rasla in se bližala vrednosti U (slika 98)[1]:
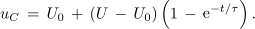
Zgled 2
Kondenzator najprej naelektrimo na polno napetost z virom napetosti U ter stikalo izključimo, nato kondenzator odklopimo in ga v obratni polariteti spet priklopimo v vezje. Njegova prednapetost U0 je tedaj ravno -U. Zatem stikalo spet vključimo. Določimo čas t*, ob katerem bo napetost kondenzatorja enaka 0 V. ⇒ Prejšnjo enačbo zapišemo za trenutek t* ter ga iz nje izračunamo:
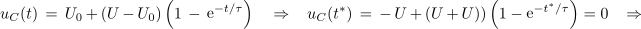
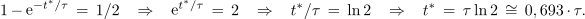
V času 69 % časovne konstante bo napetost na kondenzatorju ravno nič voltov, takoj zatem pa se bo pričela vzpenjati k vrednosti U.
V preteklih primerih smo napetostni vir smatrali za idealen, da ima notranjo upornost enako nič. Brž ko bi ne bil takšen, bi se njegova notranja upornost Rnot. pridružila upornosti polnilnega predupora. Časovna konstanta τ bi bila takrat nekoliko daljša, τ = (Rnot + R)C, enako tudi proces polnjenja, končna napetost kondenzatorja pa bi bila enaka napetosti odprtih sponk vira.
Opombe
- ↑ Rešitev je takšna, kot da bi v prejšnjih časovnih diagramih ordinatno os premaknili za čas, kateremu ustreza začetna vrednost polnilnega toka.
| | 5.8.2 Polnjenje kondenzatorja s tokovnim virom |