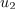Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (3 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
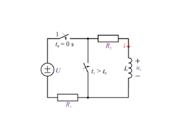
| - | Kot primer nekočljivega izklopa tuljave naj služi vezje z dvema stikaloma (slika | + | [[Slika:eele_slika_visji_104.svg|thumb|Slika 104: Tuljavino polnilno in praznilno vezje. ]] |
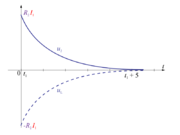
| + | [[Slika:eele_slika_visji_105.svg|thumb|Slika 105: Napetosti na elementih sta si nasprotni; nenarisani tok skozi tuljavo je sorazmeren napetosti <latex>u_2</latex>.]] | ||
| + | Kot primer nekočljivega izklopa tuljave naj služi vezje z dvema stikaloma (slika 104). Ob ''t''<sub>0</sub> = 0 s sprožimo s prvim polnjenje, ki se pri toku skozi upora in tuljavo polni s časovno konstanto ''τ''<sub>12</sub> = ''L'' / (''R''<sub>1</sub> + ''R''<sub>2</sub>), z drugim stikalom pa v trenutku ''t''<sub>1</sub> s kratkostičenjem vzpostavimo dva ločena tokokroga: v levem določata tok vir in prvi upor, v desnem tokokrogu pa se odvija praznjenje tuljave. | ||
| + | |||
Naj ima tok tuljave ob času ''t''<sub>1</sub> vrednost ''I''<sub>1</sub>. Enačba druge zanke je naslednja: | Naj ima tok tuljave ob času ''t''<sub>1</sub> vrednost ''I''<sub>1</sub>. Enačba druge zanke je naslednja: | ||
| + | |||
<latex>t\,\, \textgreater\,\, {t_1}\,:\,\,{\rm{ }}{u_2}\, +\, {u_L}\, =\, 0{\rm{ \,\,\,\,\,in \,\,\,\,\,}}{u_2}\, = \,{R_2}i{\rm{\,\,\,\,\, ter \,\,\,\,\, }}{u_L}\, = \,L\frac{{\rm{d}}i}{{\rm{d}}t}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{R_2}i\, +\, {u_L}\, =\, 0.</latex> | <latex>t\,\, \textgreater\,\, {t_1}\,:\,\,{\rm{ }}{u_2}\, +\, {u_L}\, =\, 0{\rm{ \,\,\,\,\,in \,\,\,\,\,}}{u_2}\, = \,{R_2}i{\rm{\,\,\,\,\, ter \,\,\,\,\, }}{u_L}\, = \,L\frac{{\rm{d}}i}{{\rm{d}}t}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{R_2}i\, +\, {u_L}\, =\, 0.</latex> | ||
| - | Zadnjo enačbo odvajajmo | + | |
| + | Zadnjo enačbo odvajajmo, dobimo enačbo za napetost in časovno konstanto: | ||
| + | |||
<latex>{R_2}\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, \frac{{\rm{d}}{u_L}}{{\rm{d}}t}\, =\, 0{\rm{ }} | <latex>{R_2}\frac{{\rm{d}}i}{{\rm{d}}t}\, +\, \frac{{\rm{d}}{u_L}}{{\rm{d}}t}\, =\, 0{\rm{ }} | ||
\,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}\frac{L}{R_2}\frac{{\rm{d}}{u_L}}{{\rm{d}}t}\,+\, {u_L} \,=\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{\tau _2}\, =\, \frac{L}{R_2} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{\tau _2}\frac{{\rm{d}}{u_L}}{{\rm{d}}t}\, +\, {u_L}\, =\, 0{\rm{ }}.</latex> | \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}\frac{L}{R_2}\frac{{\rm{d}}{u_L}}{{\rm{d}}t}\,+\, {u_L} \,=\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{\tau _2}\, =\, \frac{L}{R_2} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{\tau _2}\frac{{\rm{d}}{u_L}}{{\rm{d}}t}\, +\, {u_L}\, =\, 0{\rm{ }}.</latex> | ||
| + | |||
Možna rešitev za napetost na tuljavi je: | Možna rešitev za napetost na tuljavi je: | ||
| + | |||
<latex>{u_L}\, =\, B{{\mathop{\rm e}\nolimits} ^{ - t/{\tau _2}}}.</latex> | <latex>{u_L}\, =\, B{{\mathop{\rm e}\nolimits} ^{ - t/{\tau _2}}}.</latex> | ||
| + | |||
Tik po vklopu drugega stikala ima tok skozi tuljavo vrednost ''I''<sub>1</sub>, kar da: | Tik po vklopu drugega stikala ima tok skozi tuljavo vrednost ''I''<sub>1</sub>, kar da: | ||
| + | |||
<latex>t \,=\, {t_1}\, +\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{R_2}\underbrace {i({t_1}\, +\, 0)}_{I_1}\, +\, {u_L}({t_1} \,+\,0) \,= \,0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{u_L}({t_1} \,+\, 0)\, = \, - {R_2}{I_1}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}</latex> | <latex>t \,=\, {t_1}\, +\, 0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{R_2}\underbrace {i({t_1}\, +\, 0)}_{I_1}\, +\, {u_L}({t_1} \,+\,0) \,= \,0{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{u_L}({t_1} \,+\, 0)\, = \, - {R_2}{I_1}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}</latex> | ||
| + | |||
<latex>{u_L}\, =\, B{{\mathop{\rm e}\nolimits} ^{ - t/{\tau _2}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{u_L}({t_1}\, +\,0) \,=\, - {R_2}{I_1} \,= \,B{{\mathop{\rm e}\nolimits} ^{ - {t_1}/{\tau _2}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}B\, =\,- {R_2}{I_1}{{\mathop{\rm e}\nolimits} ^{{t_1}/{\tau _2}}}.</latex> | <latex>{u_L}\, =\, B{{\mathop{\rm e}\nolimits} ^{ - t/{\tau _2}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}{u_L}({t_1}\, +\,0) \,=\, - {R_2}{I_1} \,= \,B{{\mathop{\rm e}\nolimits} ^{ - {t_1}/{\tau _2}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}B\, =\,- {R_2}{I_1}{{\mathop{\rm e}\nolimits} ^{{t_1}/{\tau _2}}}.</latex> | ||
| + | |||
Napetost tuljave določa funkcija | Napetost tuljave določa funkcija | ||
| + | |||
<latex>{{u_L}\, = \, - {R_2}{I_1}{{\mathop{\rm e}\nolimits} ^{ -\, (t\, -\, {t_1})/{\tau _2}}}.}</latex> | <latex>{{u_L}\, = \, - {R_2}{I_1}{{\mathop{\rm e}\nolimits} ^{ -\, (t\, -\, {t_1})/{\tau _2}}}.}</latex> | ||
| - | Napetost na drugem uporu in tok ob praznjenju tuljave sta (slika | + | |
| + | Napetost na drugem uporu in tok ob praznjenju tuljave sta (slika 105): | ||
| + | |||
<latex>{{u_2}\, =\, - {u_L} \,= \,{R_2}{I_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t\, -\, {t_1})/{\tau _2}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}i\, =\, {u_2}/{R_2} \,=\, {I_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t\, -\, {t_1})/{\tau _2}}}.}</latex> | <latex>{{u_2}\, =\, - {u_L} \,= \,{R_2}{I_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t\, -\, {t_1})/{\tau _2}}}{\rm{ }} \,\,\,\,\,\Rightarrow\,\,\,\,\, {\rm{ }}i\, =\, {u_2}/{R_2} \,=\, {I_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t\, -\, {t_1})/{\tau _2}}}.}</latex> | ||
| - | Po nekaj časovnih konstantah se tuljava izprazni, akumulirana energija se v celoti pretvori v toploto v drugem uporu in brez nevšečnih iskrenj | + | |
| + | Po nekaj časovnih konstantah se tuljava izprazni, akumulirana energija se v celoti pretvori v toploto v drugem uporu in brez nevšečnih iskrenj lahko izklopimo obe stikali, tuljava je pripravljena za nov vklop. Zanimiv je morda še tok skozi drugo stikalo: | ||
| + | |||
<latex>{i_{\rm{s}}}\, =\, U/{R_1} \,-\, {I_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t \,-\, {t_1})/{\tau _2}}}.</latex>. | <latex>{i_{\rm{s}}}\, =\, U/{R_1} \,-\, {I_1}{{\mathop{\rm e}\nolimits} ^{ - \,(t \,-\, {t_1})/{\tau _2}}}.</latex>. | ||
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 15:58, 15. avgust 2010
![](javascript: loadPicture("Eele_slika_visji_104.svg", 800);)
![](javascript: loadPicture("Eele_slika_visji_105.svg", 800);)
Kot primer nekočljivega izklopa tuljave naj služi vezje z dvema stikaloma (slika 104). Ob t0 = 0 s sprožimo s prvim polnjenje, ki se pri toku skozi upora in tuljavo polni s časovno konstanto τ12 = L / (R1 + R2), z drugim stikalom pa v trenutku t1 s kratkostičenjem vzpostavimo dva ločena tokokroga: v levem določata tok vir in prvi upor, v desnem tokokrogu pa se odvija praznjenje tuljave.
Naj ima tok tuljave ob času t1 vrednost I1. Enačba druge zanke je naslednja:
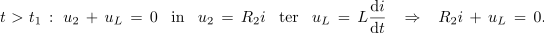
Zadnjo enačbo odvajajmo, dobimo enačbo za napetost in časovno konstanto:
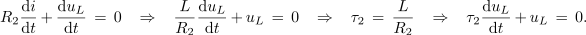
Možna rešitev za napetost na tuljavi je:
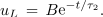
Tik po vklopu drugega stikala ima tok skozi tuljavo vrednost I1, kar da:
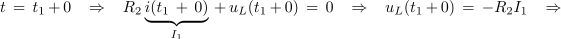
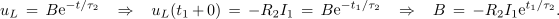
Napetost tuljave določa funkcija
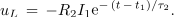
Napetost na drugem uporu in tok ob praznjenju tuljave sta (slika 105):
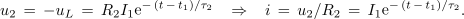
Po nekaj časovnih konstantah se tuljava izprazni, akumulirana energija se v celoti pretvori v toploto v drugem uporu in brez nevšečnih iskrenj lahko izklopimo obe stikali, tuljava je pripravljena za nov vklop. Zanimiv je morda še tok skozi drugo stikalo:
 5.11 Izklop tuljave
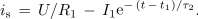
| 6 Resonančni pojavi (višji nivo)
|
