Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
| (3 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | Bočni (krožni) frekvenci <latex>f_1</latex> in <latex>f_2</latex> (<latex>\omega_1</latex> in <latex>\omega_2</latex>) sledita iz opredelitve pasovne širine in enačbe za | + | Bočni (krožni) frekvenci <latex>f_1</latex> in <latex>f_2</latex> (<latex>\omega_1</latex> in <latex>\omega_2</latex>) sledita iz opredelitve pasovne širine in enačbe za amplitudo toka v nihajnem krogu: |
| Vrstica 17: | Vrstica 17: | ||
| - | pridobimo zvezo med značilnimi frekvencami | + | pridobimo zvezo med značilnimi frekvencami: |
| - | <latex>{\omega _1 \omega _2 = \omega _0^2 {\mathrm{ } } \Rightarrow {\mathrm{ } }f_1 f_2 = f_0^2 | + | <latex>{\omega _1 \omega _2 = \omega _0^2 {\mathrm{ } } \Rightarrow {\mathrm{ } }f_1 f_2 = f_0^2 .}</latex> |
| - | + | Ko pa strani prejšnjih enačb odštejmo in upoštevamo slednjo, | |
| Vrstica 32: | Vrstica 32: | ||
| - | pridobimo še pasovno širino in kvaliteto zaporednega nihajnega kroga | + | pridobimo še pasovno širino in kvaliteto zaporednega nihajnega kroga: |
| Vrstica 38: | Vrstica 38: | ||
| - | Vloga upornosti upora je povsem očitna: čim manjša je, tem večja je kvaliteta in ožja ter ušiljena je resonančna krivulja. In ne le to | + | Vloga upornosti upora je povsem očitna: čim manjša je, tem večja je kvaliteta in ožja ter ušiljena je resonančna krivulja. In ne le to, če se s kvaliteto vrnemo k zapisom kazalcev napetosti na elementih nihajnega vezja, ugotovimo, da je kvocient amplitude napetosti na tuljavi (kondenzatorju) in napetosti na uporu (viru) v resonanci enak ravno kvaliteti. Za konec poiščimo še izraza za bočni frekvenci. Zgornjo (<latex>f_2</latex>) dobimo iz prve: |
| Vrstica 47: | Vrstica 47: | ||
| - | spodnjo (<latex>f_1</latex>) pa iz druge kvadratne enačbe | + | spodnjo (<latex>f_1</latex>) pa iz druge kvadratne enačbe: |
| Vrstica 59: | Vrstica 59: | ||
| - | <latex>f_1 \cong f_0 \left( {1 - 1/2Q} \right) | + | <latex>f_1 \cong f_0 \left( {1 - 1/2Q} \right)</latex> in <latex>f_2 \cong f_0 \left( {1 + 1/2Q} \right).</latex> |
| - | Zgled 1 | + | '''Zgled 1''' |
| + | |||
| + | Zaporedni nihajni krog, <latex>R=0,1\,{\mathrm{\Omega}}</latex>, <latex>L=10\,{\mathrm{mH}}</latex> in <latex>C=200\,{\mathrm{nF}}</latex>, vzbuja vir harmonične napetosti amplitude <latex>1,5\,{\mathrm{V}}</latex> in nastavljive frekvence. Izračunajmo resonančno frekvenco, kvaliteto, pasovno širino, približka za bočni frekvenci in še amplitudo toka pri resonančni in bočnih frekvencah. ⇒ Iz formul sledi: | ||
Trenutna redakcija s časom 12:09, 15. avgust 2010
Bočni (krožni) frekvenci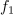
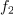
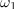
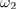
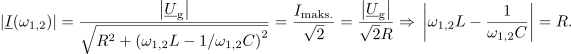
Amplituda toka zavzame mejno vrednost ravno pri frekvencah, pri katerih je absolutna vrednost skupne reaktance enaka upornosti upora. Od tod sledita:
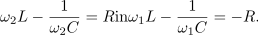
Ko strani enačb seštejemo,
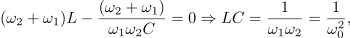
pridobimo zvezo med značilnimi frekvencami:
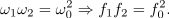
Ko pa strani prejšnjih enačb odštejmo in upoštevamo slednjo,
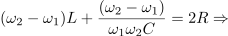
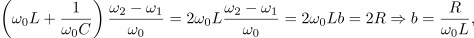
pridobimo še pasovno širino in kvaliteto zaporednega nihajnega kroga:
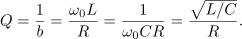
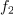
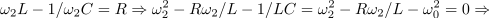
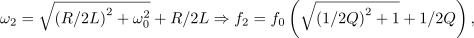
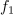
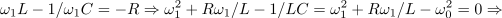
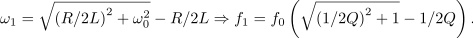
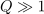
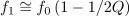
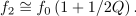
Zgled 1
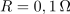
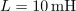
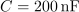
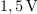
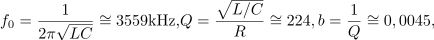

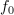
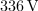
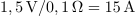
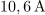
| | 6.3 Vzporedni nihajni krog in napetostna resonanca |
