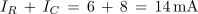|
|
| Vrstica 20: |
Vrstica 20: |
| | | | |
| | Odgovor na dobljeno tokovno neenačbo pa tudi nadaljevanje zgodbe zdaj že slutimo. | | Odgovor na dobljeno tokovno neenačbo pa tudi nadaljevanje zgodbe zdaj že slutimo. |
| - |
| |
| - |
| |
| - |
| |
| - | == Časovni potek napetosti in toka ==
| |
| - | [[Image:eele_slika_3_2_11.svg|thumb|right|Slika 3.2.11: Kazalčni diagram izmeničnega kroga z vzporedno vezavo upora in kondenzatorja]]
| |
| - |
| |
| - | '''Skupna''' količina vzporedno vezanemu uporu in kondenzatorju je električni '''tok''', zato najprej narišemo v vodoravno os koordinatnega sistema kazalec '''efektivne''' vrednosti toka (slika 3.2.11 b).
| |
| - |
| |
| - |
| |
| - | Napetost izvora požene skozi upor delovni tok '''''I<sub>R</sub>''''' in »skozi« kondenzator kapacitivni tok '''''I<sub>C</sub>'''''. Ker sta napetost in tok upora v '''fazi''', tok kondenzatorja pa '''prehiteva''' napetost za 90 °, rišemo kazalec toka '''''I<sub>R</sub>''''' na kazalec '''napetosti''' izvora, kazalec toka '''''I<sub>C</sub>''''' pa 90 ° '''pred''' kazalec napetosti izvora.
| |
| - |
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *V izmeničnem krogu z vzporedno vezavo upora in kondenzatorja sta kazalca tokov upora in kondenzatorja med seboj '''pravokotna'''.
| |
| - | *Tok '''prehiteva''' napetost izvora za fazni kot '''''φ''''', ki lahko zavzame poljubno velikost med '''0''' in '''- 90 º'''.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | <latex> - 90^{\,\circ}\,\, < \,\,\varphi \,\, <\,\, 0^{\,\circ} </latex>
| |
| - |
| |
| - |
| |
| - |
| |
| - | == Trikotnik tokov in prevodnosti ==
| |
| - | [[Image:eele_slika_3_2_12.svg|thumb|right|Slika 3.2.12: Trikotnik tokov in prevodnosti vzporedne veza upora in kondenzatorja]]
| |
| - |
| |
| - |
| |
| - | Podobno kot smo v primerih zaporednih vezav v izmeničnem krogu iz kazalčnega diagrama izrisali trikotnik napetosti, izrišemo iz kazalčnega diagrama vzporedne vezave (sl. 3.2.11 b) trikotnik tokov (sl. 3.2.12 a).
| |
| - |
| |
| - |
| |
| - |
| |
| - | Če stranice tokovnega trikotnika delimo s skupno količino vzporedne vezave, napetostjo '''''U''''',
| |
| - |
| |
| - |
| |
| - | <latex>\frac{I_R}{U}\, =\, G\,;\,\,\,\,\frac{I_L}{U}\, =\, {B_L}\,;\,\,\,\,\frac{I}{U} \,= \,Y\,,</latex>
| |
| - |
| |
| - |
| |
| - | dobimo '''podoben''' pravokotni trikotnik (sl. 3.2.12 b), katerega stranice so '''prevodnosti''' kroga.
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Toki in prevodnosti v izmeničnem krogu z vzporedno vezavo upora in kondenzatorja tvorijo pravokotna trikotnika.
| |
| - | *Efektivni tok izvora je enak '''geometrični''' vsoti efektivnih tokov, prevodnost vezave pa '''geometrični''' vsoti prevodnosti vzporedno vezanih upora in kondenzatorja.
| |
| - | *Prevodnosti vezave '''''Y''''' (S) pravimo '''admitanca'''.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | <latex>I\, = \,\sqrt {{I_R}^2 \,+\, {I_C}^2} \,;\,\,\,\,Y\, =\, \sqrt {{G^2}\, +\, {B_C}^2}\, \,\,...</latex>
| |
| - |
| |
| - | Pri računanju faznega kota ali s faznim kotom pa velja npr.:
| |
| - |
| |
| - | <latex>\csc \varphi \, = \,\frac{I_R}{I}\, =\, \frac{G}{Y}\,;\,\,\,\,\tan \varphi \, =\, \frac{B_C}{G}\,\,\,\,...\,\,\,\, \Rightarrow\,\,\,\, \varphi </latex>
| |
| - |
| |
| - | Že pri prvi vzporedni vezavi omenimo dejstva, ki jih zaradi enostavnosti pozneje ne bomo omenjali:
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Trikotnik tokov velja za efektivne in maksimalne vrednosti tokov.
| |
| - | *Trenutne vrednosti izmeničnih tokov vzporedno vezanih elementov seštevamo '''aritmetično'''.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | '''Primera:'''
| |
| - |
| |
| - | <primer>
| |
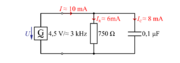
| - | 1. Vzporedna vezava upora z upornostjo 3 kΩ in kondenzatorja s kapacitivno upornostjo 4 kΩ je priključena na izmenično napetost 3 V. Izračunaj toke, admitanco in impedanco ter fazni kot, ki ga povzroča vezava.|||
| |
| - | <latex>{I_R}\, =\, \frac{U}{R} \,=\, \frac{3}{3000}\, =\, 1\,{\rm{mA}}</latex>
| |
| - |
| |
| - | <latex>{I_C} \,=\, \frac{U}{X_C}\, =\, \frac{3}{4000}\, =\,{\rm{0,75\,mA}}</latex>
| |
| - |
| |
| - | <latex>I\, =\, \sqrt {{I_R}^2\, +\, {I_C}^2} \, = \,\sqrt {{1^2}\, + \,{{{\rm{0,75}}}^2}} \, = {\rm{1,25}}\,{\rm{mA}}</latex>
| |
| - |
| |
| - | <latex>Y \,=\, \frac{I}{U} \,=\, \frac{{{\rm{1,25}} \,\cdot\, {{10}^{-3}}}}{3}\, =\, {\rm{0,41\,mS}}\,;\,\,\,\,Z\, =\, \frac{1}{Y} \,= \,\frac{1}{{{\rm{0,41}} \,\cdot\, {{10}^{-3}}}} \,= \,{\rm{2,4\,k}}\Omega </latex>
| |
| - |
| |
| - | <latex>\tan \varphi\, =\, - \frac{I_C}{I_R}\, =\, - \frac{{\rm{0,75}}}{1} \,=\, - {\rm{0,75}}\,\,\,\, \Rightarrow\,\,\,\, \varphi \, =\, - 36^{\,\circ} </latex>
| |
| - | </primer>
| |
| - |
| |
| - | <primer>
| |
| - | 2. Vzporedna vezava upora in kondenzatorja je priključena na sinusno napetost s frekvenco 50 kHz. Kolikšna je kapacitivnost kondenzatorja, če je tok izvora 75,8 mA in tok upora 23 mA, upornost upora pa je 10 kΩ?|||
| |
| - | <latex>I\, =\, \sqrt {{I_R}^2 \,+\, {I_C}^2} \,\,\,\, \Rightarrow\,\,\,\, {I_C}\, =\, \sqrt {{I^2} \,-\, {I_R}^2} \, = \,\sqrt {{{{\rm{78,5}}}^2}\, - \,{{23}^2}} \, =\,{\rm{72,2\,mA}}</latex>
| |
| - |
| |
| - | <latex>{U_R}\, =\, U\, =\, {I_R} \,\cdot\, R \,= \,23\, \cdot\, {10^{-3}} \,\cdot \,10 \,\cdot\, {10^3}\, = \,230{\rm{\,V}}</latex>
| |
| - |
| |
| - | <latex>{X_C}\, = \,\frac{U}{I_C}\, =\, \frac{230}{{\rm{72,2}} \,\cdot\, {10}^{-3}}\, = \,{\rm{3,2\,k\Omega }}</latex>
| |
| - |
| |
| - | <latex>{X_C}\, =\, \frac{1}{2\pi fC}\,\,\,\, \Rightarrow \,\,\,\,C\, =\, \frac{1}{2\pi f{X_C}} \,=\, \frac{1}{2\pi\,\cdot \,50\, \cdot \,{{10}^3} \,\cdot\, {\rm{3,2}}\, \cdot\, {{10}^3}}\, =\, 1\,{\rm{nF}}</latex>
| |
| - | </primer>
| |
| | | | |
| | | | |
| | {{Hierarchy footer}} | | {{Hierarchy footer}} |
![](javascript: loadPicture("Eele_slika_3_2_10.svg", 800);)
3.2.2.3 Zaporedna RLC vezava (interaktivna simulacija)
