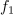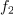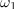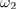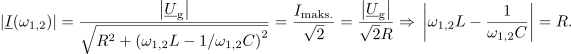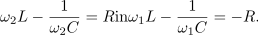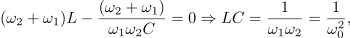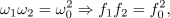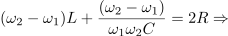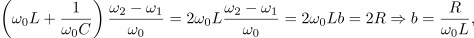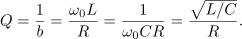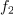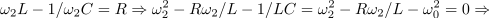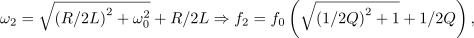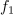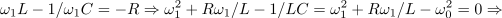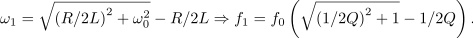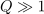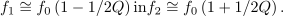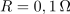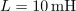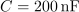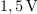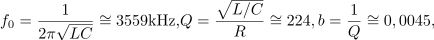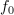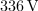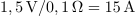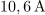Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
Redakcija: 16:09, 14. maj 2010
Bočni (krožni) frekvenci
in
(
in
) sledita iz opredelitve pasovne širine in enačbe za ampitudo toka v nihajnem krogu:
Amplituda toka zavzame mejno vrednost ravno pri frekvencah, pri katerih je absolutna vrednost skupne reaktance enaka upornosti upora. Od tod sledita:
Ko strani enačb seštejemo,
pridobimo zvezo med značilnimi frekvencami,
ko pa strani prejšnjih enačb odštejmo in upoštevamo slednjo,
pridobimo še pasovno širino in kvaliteto zaporednega nihajnega kroga,
Vloga upornosti upora je povsem očitna: čim manjša je, tem večja je kvaliteta in ožja ter ušiljena je resonančna krivulja. In ne le to: če se s kvaliteto vrnemo k zapisom kazalcev napetosti na elementih nihajnega vezja, ugotovimo, da je kvocient amplitude napetosti na tuljavi (kondenzatorju) in napetosti na uporu (viru) v resonanci enak ravno kvaliteti. Za konec poiščimo še izraza za bočni frekvenci! Zgornjo (
) dobimo iz prve,
spodnjo (
) pa iz druge kvadratne enačbe,
Pri zelo kvalitetnem (selektivnem) nihajnem krogu (
) leži resonančna frekvenca praktično v sredini intervala pasovne širine, saj je vrednost korena takrat praktično ena; aproksimativni vrednosti bočnih frekvenc sta:
Zgled 1. Zaporedni nihajni krog,
,
in
, vzbuja vir harmonične napetosti amplitude
in nastavljive frekvence. Izračunajmo resonančno frekvenco, kvaliteto, pasovno širino, približka za bočni frekvenci in še amplitudo toka pri resonančni in bočnih frekvencah! ⇒ Iz formul sledi:
Če bo nihajni krog vzbujan s frekvenco
, bosta amplitudi napetosti na tuljavi in kondenzatorju 224-kratnik amplitude napetosti vira, torej
. Amplituda toka v resonanci je
, pri bočnih frekvencah pa približno
.
6.2.1 Resonančna krivulja, pasovna širina in kvaliteta nihajnega kroga
