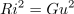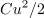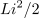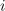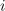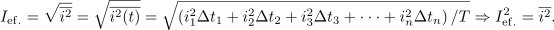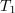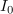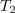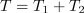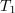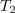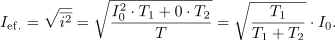Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
|
|
| Vrstica 15: |
Vrstica 15: |
| | Primer: Pri sklenjenem stikalu je tok skozi upor upornosti 20 Ω enak 3 A; pretikalo stikala preklapljamo tako, da je stikalo 1 s sklenjeno, 3 s pa razklenjeno. Efektivna vrednost toka je torej 1,5 A, srednja moč v uporu pa (1,5 A)<sup>2</sup> · 20 Ω = 45 W.<br> | | Primer: Pri sklenjenem stikalu je tok skozi upor upornosti 20 Ω enak 3 A; pretikalo stikala preklapljamo tako, da je stikalo 1 s sklenjeno, 3 s pa razklenjeno. Efektivna vrednost toka je torej 1,5 A, srednja moč v uporu pa (1,5 A)<sup>2</sup> · 20 Ω = 45 W.<br> |
| | | | |
| - |
| |
| - | == Efektivna vrednost harmonične funkcije ==
| |
| - | Pri harmonični napetosti (toku)
| |
| - |
| |
| - |
| |
| - | <latex>u = u(t) = U_{\mathrm{m} } \cos (\omega t + \alpha _u ),</latex>
| |
| - |
| |
| - |
| |
| - | bomo postopali nekoliko drugače in se izognili nepregledni vsoti. Pišimo:<ref><latex>2\cos ^2 x = (1 + \cos 2x).</latex></ref>
| |
| - |
| |
| - |
| |
| - | <latex>U_{ {\mathrm{ef} }{\mathrm{.} } }^{\mathrm{2} } = \overline {u^2 } = \overline {U_{\mathrm{m} }^{\mathrm{2} } \cos ^2 (\omega t + \alpha _u )} = \overline { {\textstyle{\frac{1}{2} } }\left( {1 + \cos 2(\omega t + \alpha _u )} \right)} U_{\mathrm{m} }^{\mathrm{2} } = </latex>
| |
| - |
| |
| - |
| |
| - | <latex>{\textstyle{\frac{1}{2} } }\left( {1 + \overline {\cos 2(\omega t + \alpha _i )} } \right)U_{\mathrm{m} }^{\mathrm{2} } = {\textstyle{\frac{1}{2} } }U_{\mathrm{m} }^{\mathrm{2} } .</latex>
| |
| - |
| |
| - |
| |
| - | Izraz pod črto smo preoblikovali, se sklicevali na ničelno srednjo vrednost harmonične funkcije in dobili zelo enostaven rezultat:
| |
| - |
| |
| - |
| |
| - | <latex>{U_{ {\mathrm{ef} }{\mathrm{.} } } = U_{\mathrm{m} } /\sqrt {\mathrm{2} } \cong {\mathrm{0,707} }U_{\mathrm{m} } {\mathrm{ } } \Rightarrow {\mathrm{ } }U_{\mathrm{m} } = \sqrt {\mathrm{2} } U_{ {\mathrm{ef} }{\mathrm{.} } } \cong {\mathrm{1,414} }U_{ {\mathrm{ef} }{\mathrm{.} } } .}</latex>
| |
| - |
| |
| - |
| |
| - | Efektivna vrednost sinusne funkcije ustreza (okoli) 71 % temenske vrednosti.
| |
| - |
| |
| - |
| |
| - | <references />
| |
| | | | |
| | {{Hierarchy footer}} | | {{Hierarchy footer}} |
Redakcija: 12:50, 27. junij 2010
Moč v uporu,
, energija v kondenzatorju,
in energija v tuljavi,
so sorazmerne kvadratu toka oziroma napetosti. Če bosta napetost na kondenzatorju (ali uporu) ali tok skozi tuljavo (ali upor) periodična, bosta takšni tudi ustrezni energiji oziroma moč; smiselno je torej govoriti o poprečjih moči in energij oziroma o srednjih vrednostih kvadrata napetosti in kvadrata toka. Kvadratna korena teh srednjih vrednosti določata novi značilnici; imenujemo ju
efektivna vrednost toka
in
efektivna vrednost napetosti
. Če ostaja delitev periode enaka kot pri srednji vrednosti, potem določa efektivno vrednost toka
tale izraz:
Zgled 3
Začnimo z impulznim tokom. Naj je čas
trajanje impulza jakosti
,
pa čas pavze, da npr. pretikalo stikala v vodniku dvovoda med uporom in virom izmenjaje preklapljamo (slika 5). Določimo efektivno vrednost toka. ⇒ Perioda
. Zaradi impulznosti zadostuje periodo razdeliti na dva intervala, trajanj
in
. Za efektivno vrednost toka dobimo tole formulo:
Primer: Pri sklenjenem stikalu je tok skozi upor upornosti 20 Ω enak 3 A; pretikalo stikala preklapljamo tako, da je stikalo 1 s sklenjeno, 3 s pa razklenjeno. Efektivna vrednost toka je torej 1,5 A, srednja moč v uporu pa (1,5 A)2 · 20 Ω = 45 W.
Podpoglavja: