Iz e-ELEKTROTEHNIKA plus
| Vrstica 10: | Vrstica 10: | ||
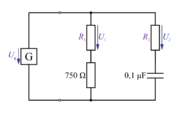
Sestavimo vezje, ki ga prikazuje sl. 1.25, in ga priključimo na sinusno napetost funkcijskega generatorja 5 V/1000 Hz. Z dvokanalnim osciloskopom primerjajmo časovna poteka padcev napetosti na uporih ''R''<sub>1</sub> = ''R''<sub>2</sub> = ''R''<sub>3</sub> = 1 kΩ s časovnim potekom napetosti generatorja ''U<sub>g</sub>'' (sl. 1.26). | Sestavimo vezje, ki ga prikazuje sl. 1.25, in ga priključimo na sinusno napetost funkcijskega generatorja 5 V/1000 Hz. Z dvokanalnim osciloskopom primerjajmo časovna poteka padcev napetosti na uporih ''R''<sub>1</sub> = ''R''<sub>2</sub> = ''R''<sub>3</sub> = 1 kΩ s časovnim potekom napetosti generatorja ''U<sub>g</sub>'' (sl. 1.26). | ||
| - | *Izmenični napetosti na elementih vezave imajo enako | + | *Izmenični napetosti na elementih vezave imajo enako '''sinusno''' obliko ter enako '''periodo''' in '''frekvenco''' kot izvor napetosti. |
*Časovni potek napetosti na ''R''<sub>1</sub> je tudi časovno skladen z ''U<sub>g</sub>'', kar pa za vejo s kapacitivnostjo ne velja. | *Časovni potek napetosti na ''R''<sub>1</sub> je tudi časovno skladen z ''U<sub>g</sub>'', kar pa za vejo s kapacitivnostjo ne velja. | ||
</poskus> | </poskus> | ||
| Vrstica 18: | Vrstica 18: | ||
<pomembno> | <pomembno> | ||
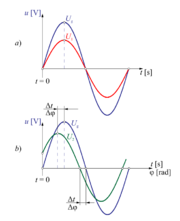
| - | *Izmenični količini '''enakih frekvenc''', ki imata v vsakem trenutku '''enako smer''' (sl. 1.26), sta v '''fazi'''<ref>phasis, gr. pojav, stanje, določeno s frekvenco in začetnim položajem</ref>. | + | *Izmenični količini '''enakih frekvenc''', ki imata v vsakem trenutku '''enako smer''' (sl. 1.26), sta v '''fazi'''<ref>phasis, gr. = pojav, stanje, določeno s frekvenco in začetnim položajem</ref>. |
| - | *Če izmenični količini spremenita smer z določeno '''časovno''' razliko '''Δ t''' (sl. 1.26) pravimo, da je med njima '''fazni premik'''. | + | *Če izmenični količini spremenita smer z določeno '''časovno''' razliko '''Δ t''' (sl. 1.26), pravimo, da je med njima '''fazni premik'''. |
*Če izmenična količina spremeni smer '''prej''' kot druga, pravimo, da '''prehiteva''' drugo količino in obratno (sl. 1.26). | *Če izmenična količina spremeni smer '''prej''' kot druga, pravimo, da '''prehiteva''' drugo količino in obratno (sl. 1.26). | ||
| Vrstica 27: | Vrstica 27: | ||
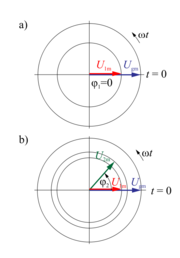
| - | Zahtevno risanje '''časovnih''' diagramov je tem bolj zamudno, čim več količin želimo prikazati. Kot vemo (pogl. 1.2, sl. 1.13), za prakso zadostuje, če '''sinusne''' količine '''enakih frekvenc''' predstavimo v '''kazalčnem''' diagramu (sl. 1.27). Zaradi enostavnejšega razumevanja prehoda iz časovnega v kazalčni diagram | + | Zahtevno risanje '''časovnih''' diagramov je tem bolj zamudno, čim več količin želimo prikazati. Kot vemo (pogl. 1.2, sl. 1.13), za prakso zadostuje, če '''sinusne''' količine '''enakih frekvenc''' predstavimo v '''kazalčnem''' diagramu (sl. 1.27). Zaradi enostavnejšega razumevanja prehoda iz časovnega v kazalčni diagram je na sl. 1.27 prikazana '''časovna''' odvisnost položaja kazalcev. Položaj kazalcev ustreza trenutku '''''t'' = 0''' v časovnem diagramu na sl. 1.26. |
| - | V praksi fazne premike izmeničnih količin pogosto obravnavamo tudi s '''koti'''. Oglejmo '''splošni primer''' v trenutku ''t'' = 0 »posnetih« kazalcev npr. dveh izmeničnih napetosti s faznim premikom (sl. 1.28). Kazalca smo ujeli med rotacijo kar pomeni, da sta do trenutka posnetka (''t'' = 0) | + | V praksi fazne premike izmeničnih količin pogosto obravnavamo tudi s '''koti'''. Oglejmo si '''splošni primer''' v trenutku ''t'' = 0 »posnetih« kazalcev npr. dveh izmeničnih napetosti s faznim premikom (sl. 1.28). Kazalca smo ujeli med rotacijo, kar pomeni, da sta do trenutka posnetka (''t'' = 0) že ustvarila kota ''α''<sub>02</sub> in ''α''<sub>01</sub>. Glede na začetek našega opazovanja (''t'' = 0) jima pravimo '''začetna kota'''. Pri tem ni pomembno, kolikšna sta, ampak le njuna '''razlika'''. |
<pomembno> | <pomembno> | ||
*Trenutni vrednosti izmeničnih količin, katerih kazalca imata '''enaka''' začetna kota, imata v vsakem trenutku '''enako smer''', zato pravimo, da sta v '''fazi'''. | *Trenutni vrednosti izmeničnih količin, katerih kazalca imata '''enaka''' začetna kota, imata v vsakem trenutku '''enako smer''', zato pravimo, da sta v '''fazi'''. | ||
| - | *Izmenična količina z '''večjim''' začetnim kotom (sl. 1.27) | + | *Izmenična količina z '''večjim''' začetnim kotom (sl. 1.27) '''prej spremeni smer''', zato pravimo, da '''prehiteva''' drugo izmenično količino in obratno. |
</pomembno> | </pomembno> | ||
| Vrstica 89: | Vrstica 89: | ||
| - | Kljub svoji preprostosti | + | Kljub svoji preprostosti omogočajo kazalčni diagrami pregledno obravnavo tudi '''zahtevnejših''' sestavljenih izmeničnih krogov. Zato bo kazalčni diagram naše osnovno »'''orodje'''« za obdelavo izmeničnih krogov. Če nas moti vrtenje kazalcev, jih lahko brez škode »ustavimo« tako, da se »usedemo« npr. na kazalec toka in se z njimi »zapeljemo« okrog koordinatnega izhodišča. Bistva diagrama s tem nismo prizadeli, izničili pa smo relativno hitrost kazalcev glede na opazovalca in omogočili delo z »'''mirujočimi'''« kazalci. Pri znanih faznih premikih lahko »pozabimo« tudi na začetne kote. |
Redakcija: 09:41, 7. maj 2010
![](javascript: loadPicture("Eele_slika_1_2.svg", 801);)
![](javascript: loadPicture("Eele_slika_1_13.svg", 622);)
![](javascript: loadPicture("Eele_slika_1_25.svg", 648);)
![](javascript: loadPicture("Eele_slika_1_26.svg", 696);)
![](javascript: loadPicture("Eele_slika_1_27.svg", 480);)
Poskus 1.3:
Sestavimo vezje, ki ga prikazuje sl. 1.25, in ga priključimo na sinusno napetost funkcijskega generatorja 5 V/1000 Hz. Z dvokanalnim osciloskopom primerjajmo časovna poteka padcev napetosti na uporih R1 = R2 = R3 = 1 kΩ s časovnim potekom napetosti generatorja Ug (sl. 1.26).
- Izmenični napetosti na elementih vezave imajo enako sinusno obliko ter enako periodo in frekvenco kot izvor napetosti.
- Časovni potek napetosti na R1 je tudi časovno skladen z Ug, kar pa za vejo s kapacitivnostjo ne velja.
Podobne primere imamo v električnih krogih električnih naprav in strojev, ki imajo poleg ohmske upornosti tudi kapacitivno in induktivno lastnost. Taki premiki časovnih potekov izmeničnih količin enakih frekvenc so pogosto osnova delovanja električne naprave ali stroja in so ustvarjeni namenoma. Pogosto pa so posledica neželene kapacitivne in induktivne lastnosti izmeničnih krogov in so za delovanje električnih strojev in naprav škodljivi.
- Izmenični količini enakih frekvenc, ki imata v vsakem trenutku enako smer (sl. 1.26), sta v fazi[1].
- Če izmenični količini spremenita smer z določeno časovno razliko Δ t (sl. 1.26), pravimo, da je med njima fazni premik.
- Če izmenična količina spremeni smer prej kot druga, pravimo, da prehiteva drugo količino in obratno (sl. 1.26).
Zahtevno risanje časovnih diagramov je tem bolj zamudno, čim več količin želimo prikazati. Kot vemo (pogl. 1.2, sl. 1.13), za prakso zadostuje, če sinusne količine enakih frekvenc predstavimo v kazalčnem diagramu (sl. 1.27). Zaradi enostavnejšega razumevanja prehoda iz časovnega v kazalčni diagram je na sl. 1.27 prikazana časovna odvisnost položaja kazalcev. Položaj kazalcev ustreza trenutku t = 0 v časovnem diagramu na sl. 1.26.
V praksi fazne premike izmeničnih količin pogosto obravnavamo tudi s koti. Oglejmo si splošni primer v trenutku t = 0 »posnetih« kazalcev npr. dveh izmeničnih napetosti s faznim premikom (sl. 1.28). Kazalca smo ujeli med rotacijo, kar pomeni, da sta do trenutka posnetka (t = 0) že ustvarila kota α02 in α01. Glede na začetek našega opazovanja (t = 0) jima pravimo začetna kota. Pri tem ni pomembno, kolikšna sta, ampak le njuna razlika.
- Trenutni vrednosti izmeničnih količin, katerih kazalca imata enaka začetna kota, imata v vsakem trenutku enako smer, zato pravimo, da sta v fazi.
- Izmenična količina z večjim začetnim kotom (sl. 1.27) prej spremeni smer, zato pravimo, da prehiteva drugo izmenično količino in obratno.
V splošnem primeru izmenična količina z večjim začetnim kotom prehiteva izmenično količino z manjšim začetnim kotom za razliko začetnih kotov α.
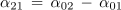
- Razliko začetnih kotov izmeničnih količin enakih frekvenc imenujemo fazni premik omenjenih količin.
Na področju elektroenergetike se najpogosteje srečujemo s faznim premikom med tokom in napetostjo (sl. 1.28). Spoznali bomo, da sta od njega močno odvisna delo in moč izmeničnega toka, pa tudi izgube električne energije v električnih napravah in omrežjih. Zato mu dajemo poseben pomen.
- Fazni premik med tokom in napetostjo imenujemo fazni kot.
- Fazni kot označujemo s črko φ, merimo pa v kotnih stopinjah.
Enačbi tako predstavljenih sinusnih napetosti in toka se glasita:
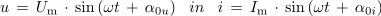
- Fazni kot je določen z razliko začetnih kotov napetosti in toka.
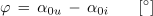
- Po dogovoru označujemo fazni kot z ločno puščico v smeri od kazalca toka proti kazalcu napetosti (sl. 1.28).
- Če tok zaostaja za napetostjo je, po dogovoru, fazni kot pozitiven, sicer pa je negativen.
Iz slik 1.26, 1.27 in 1,28 lahko še sklepamo:
- Kazalci vseh količin z enako frekvenco se v kazalčnem diagramu vrtijo v isti smeri z enako krožno frekvenco ω.
- Fazni premiki med kazalci se med vrtenjem kazalcev ohranjajo.
- Kazalca količin, ki sta v fazi, se prekrivata.
Kljub svoji preprostosti omogočajo kazalčni diagrami pregledno obravnavo tudi zahtevnejših sestavljenih izmeničnih krogov. Zato bo kazalčni diagram naše osnovno »orodje« za obdelavo izmeničnih krogov. Če nas moti vrtenje kazalcev, jih lahko brez škode »ustavimo« tako, da se »usedemo« npr. na kazalec toka in se z njimi »zapeljemo« okrog koordinatnega izhodišča. Bistva diagrama s tem nismo prizadeli, izničili pa smo relativno hitrost kazalcev glede na opazovalca in omogočili delo z »mirujočimi« kazalci. Pri znanih faznih premikih lahko »pozabimo« tudi na začetne kote.
Opombe
- ↑ phasis, gr. = pojav, stanje, določeno s frekvenco in začetnim položajem
 1.4 Srednja vrednost periodične količine
| 1.6 Seštevanje izmeničnih količin
|
