Iz e-ELEKTROTEHNIKA plus
| Vrstica 17: | Vrstica 17: | ||
<pomembno> | <pomembno> | ||
| - | *V izmeničnem krogu z '''vzporedno''' vezavo upora in kondenzatorja je efektivni tok izvora '''večji''' od '''aritmetične''' vsote tokov '''''I<sub>R</sub>''''' in '''''I<sub>C</sub>''''' | + | *V izmeničnem krogu z '''vzporedno''' vezavo upora in kondenzatorja je efektivni tok izvora '''večji''' od '''aritmetične''' vsote tokov '''''I<sub>R</sub>''''' in '''''I<sub>C</sub>''''' skozi '''upor''' in '''kondenzator'''. |
</pomembno> | </pomembno> | ||
| - | Odgovor na dobljeno tokovno neenačbo pa tudi nadaljevanje zgodbe | + | Odgovor na dobljeno tokovno neenačbo pa tudi nadaljevanje zgodbe zdaj že slutimo. |
| Vrstica 28: | Vrstica 28: | ||
| - | '''Skupna''' količina vzporedno | + | '''Skupna''' količina vzporedno vezanemu uporu in kondenzatorju je električni '''tok''', zato najprej narišemo v vodoravno os koordinatnega sistema kazalec '''efektivne''' vrednosti toka (slika 3.2.11 b). |
| Vrstica 48: | Vrstica 48: | ||
| - | Podobno kot smo v primerih zaporednih vezav v izmeničnem krogu iz kazalčnega diagrama izrisali trikotnik napetosti, izrišemo iz kazalčnega diagrama vzporedne vezave (sl. 3.2.11 b) | + | Podobno kot smo v primerih zaporednih vezav v izmeničnem krogu iz kazalčnega diagrama izrisali trikotnik napetosti, izrišemo iz kazalčnega diagrama vzporedne vezave (sl. 3.2.11 b) trikotnik tokov (sl. 3.2.12 a). |
| Vrstica 68: | Vrstica 68: | ||
| - | <latex>I\, = \,\sqrt {{I_R}^2 \,+\, {I_C}^2} \,;\,\,\,\,Y\, =\, \sqrt {{G^2}\, +\, {B_C}^2} | + | <latex>I\, = \,\sqrt {{I_R}^2 \,+\, {I_C}^2} \,;\,\,\,\,Y\, =\, \sqrt {{G^2}\, +\, {B_C}^2}\, \,\,...</latex> |
Pri računanju faznega kota ali s faznim kotom pa velja npr.: | Pri računanju faznega kota ali s faznim kotom pa velja npr.: | ||
| Vrstica 74: | Vrstica 74: | ||
<latex>\csc \varphi \, = \,\frac{I_R}{I}\, =\, \frac{G}{Y}\,;\,\,\,\,\tan \varphi \, =\, \frac{B_C}{G}\,\,\,\,...\,\,\,\, \Rightarrow\,\,\,\, \varphi </latex> | <latex>\csc \varphi \, = \,\frac{I_R}{I}\, =\, \frac{G}{Y}\,;\,\,\,\,\tan \varphi \, =\, \frac{B_C}{G}\,\,\,\,...\,\,\,\, \Rightarrow\,\,\,\, \varphi </latex> | ||
| - | Že pri prvi vzporedni vezavi omenimo dejstva, ki jih zaradi enostavnosti | + | Že pri prvi vzporedni vezavi omenimo dejstva, ki jih zaradi enostavnosti pozneje ne bomo omenjali: |
Redakcija: 17:23, 7. maj 2010
![](javascript: loadPicture("Eele_slika_3_2_10.svg", 800);)
![](javascript: loadPicture("Eele_slika_3_2_11.svg", 955);)
![](javascript: loadPicture("Eele_slika_3_2_12.svg", 816);)
Poskus 2.2.3:
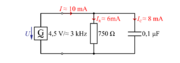
Vzporedno vezavo upora z upornostjo 750 Ω in kondenzatorja s kapacitivnostjo 0,1 µF priključimo na sinusno napetost 4,5 V/3 kHz (sl. 3.2.10).
Izmerimo tok IR, IC in I ter izmerjeno preverimo z zakonom tokovnega vozlišča:
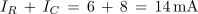
- V izmeničnem krogu z vzporedno vezavo upora in kondenzatorja je efektivni tok izvora večji od aritmetične vsote tokov IR in IC skozi upor in kondenzator.
Odgovor na dobljeno tokovno neenačbo pa tudi nadaljevanje zgodbe zdaj že slutimo.
Časovni potek napetosti in toka
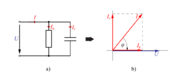
Skupna količina vzporedno vezanemu uporu in kondenzatorju je električni tok, zato najprej narišemo v vodoravno os koordinatnega sistema kazalec efektivne vrednosti toka (slika 3.2.11 b).
Napetost izvora požene skozi upor delovni tok IR in »skozi« kondenzator kapacitivni tok IC. Ker sta napetost in tok upora v fazi, tok kondenzatorja pa prehiteva napetost za 90 °, rišemo kazalec toka IR na kazalec napetosti izvora, kazalec toka IC pa 90 ° pred kazalec napetosti izvora.
- V izmeničnem krogu z vzporedno vezavo upora in kondenzatorja sta kazalca tokov upora in kondenzatorja med seboj pravokotna.
- Tok prehiteva napetost izvora za fazni kot φ, ki lahko zavzame poljubno velikost med 0 in - 90 º.
Trikotnik tokov in prevodnosti
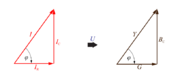
Podobno kot smo v primerih zaporednih vezav v izmeničnem krogu iz kazalčnega diagrama izrisali trikotnik napetosti, izrišemo iz kazalčnega diagrama vzporedne vezave (sl. 3.2.11 b) trikotnik tokov (sl. 3.2.12 a).
Če stranice tokovnega trikotnika delimo s skupno količino vzporedne vezave, napetostjo U,
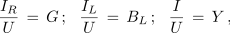
dobimo podoben pravokotni trikotnik (sl. 3.2.12 b), katerega stranice so prevodnosti kroga.
- Toki in prevodnosti v izmeničnem krogu z vzporedno vezavo upora in kondenzatorja tvorijo pravokotna trikotnika.
- Efektivni tok izvora je enak geometrični vsoti efektivnih tokov, prevodnost vezave pa geometrični vsoti prevodnosti vzporedno vezanih upora in kondenzatorja.
- Prevodnosti vezave Y (S) pravimo admitanca.
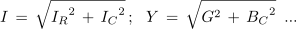
Pri računanju faznega kota ali s faznim kotom pa velja npr.:
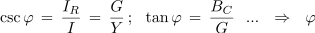
Že pri prvi vzporedni vezavi omenimo dejstva, ki jih zaradi enostavnosti pozneje ne bomo omenjali:
- Trikotnik tokov velja za efektivne in maksimalne vrednosti tokov.
- Trenutne vrednosti izmeničnih tokov vzporedno vezanih elementov seštevamo aritmetično.
Primera:
Primer:
1. Vzporedna vezava upora z upornostjo 3 kΩ in kondenzatorja s kapacitivno upornostjo 4 kΩ je priključena na izmenično napetost 3 V. Izračunaj toke, admitanco in impedanco ter fazni kot, ki ga povzroča vezava.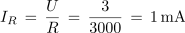
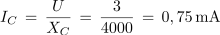
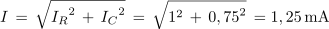
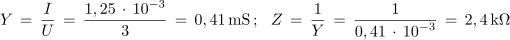
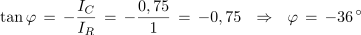
Primer:
2. Vzporedna vezava upora in kondenzatorja je priključena na sinusno napetost s frekvenco 50 kHz. Kolikšna je kapacitivnost kondenzatorja, če je tok izvora 75,8 mA in tok upora 23 mA, upornost upora pa je 10 kΩ?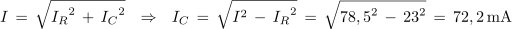
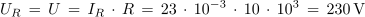
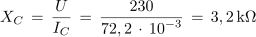
Podpoglavja:
 3.2.2.3 Zaporedna RLC vezava (interaktivna simulacija)
| 3.2.3.1 Časovni potek napetosti in toka....
|
