Iz e-ELEKTROTEHNIKA plus
(Nova stran z vsebino: Slika 3.1.3: Primerjava časovnih potekov napetosti v ohmskem izmeničnem krogu [[Image:eele_slika_3_1_4.svg|thumb|right|Slika 3.1.4:…) |
|||
| Vrstica 12: | Vrstica 12: | ||
Prek padca napetosti na ohmski upornosti '''posredno''' opazujemo tudi časovni potek toka. Iz do sedaj spoznanih dejstev o električnem toku namreč vemo, da je tok skozi konstantno ohmsko upornost premo sorazmeren z napetostjo: | Prek padca napetosti na ohmski upornosti '''posredno''' opazujemo tudi časovni potek toka. Iz do sedaj spoznanih dejstev o električnem toku namreč vemo, da je tok skozi konstantno ohmsko upornost premo sorazmeren z napetostjo: | ||
| + | |||
<latex>i\,=\, \frac {u}{R}</latex> | <latex>i\,=\, \frac {u}{R}</latex> | ||
| Vrstica 17: | Vrstica 18: | ||
Prepričali se bomo, da plastne upore, kot sta upora v poskusu 3.1.2, lahko pri nizki frekvenci obravnavamo kot upora s praktično čisto ohmsko upornostjo (idealna upora). Zato lahko sklepamo: | Prepričali se bomo, da plastne upore, kot sta upora v poskusu 3.1.2, lahko pri nizki frekvenci obravnavamo kot upora s praktično čisto ohmsko upornostjo (idealna upora). Zato lahko sklepamo: | ||
| + | |||
<pomembno> | <pomembno> | ||
| Vrstica 23: | Vrstica 25: | ||
Velja tudi obratno: | Velja tudi obratno: | ||
| - | |||
| Vrstica 33: | Vrstica 34: | ||
O ugotovitvi se lahko prepričamo tudi po matematični poti. V Ohmov zakon za trenutno vrednost toka | O ugotovitvi se lahko prepričamo tudi po matematični poti. V Ohmov zakon za trenutno vrednost toka | ||
| + | |||
<latex>i\,=\, \frac {u}{R}</latex> | <latex>i\,=\, \frac {u}{R}</latex> | ||
| Vrstica 38: | Vrstica 40: | ||
vstavimo izraz za trenutno vrednost sinusne napetost ''u'' = ''U''<sub>m</sub> ∙ sin (''ωt''): | vstavimo izraz za trenutno vrednost sinusne napetost ''u'' = ''U''<sub>m</sub> ∙ sin (''ωt''): | ||
| + | |||
<latex>i\,=\, \frac {U_{\rm{m}}\, \cdot\,{\rm{sin}}\,(\omega t) }{R}\, = \,\frac {U_{\rm{m}}}{R}\, \cdot\,{\rm{sin}}\,(\omega t) </latex> | <latex>i\,=\, \frac {U_{\rm{m}}\, \cdot\,{\rm{sin}}\,(\omega t) }{R}\, = \,\frac {U_{\rm{m}}}{R}\, \cdot\,{\rm{sin}}\,(\omega t) </latex> | ||
| + | |||
<latex>i\, = \,I_{\rm{m}}\, \cdot\,{\rm{sin}}\,(\omega t) </latex> | <latex>i\, = \,I_{\rm{m}}\, \cdot\,{\rm{sin}}\,(\omega t) </latex> | ||
Redakcija: 08:50, 11. maj 2010
Poskus 3.1.2:
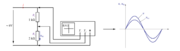
Na izvor sinusne izmenične napetosti npr. 6 V /50 Hz priključimo zaporedno vezavo plastnih uporov 1000 Ω in 2000 Ω (slika 3.1.3). Na dvokanalnem osciloskopu primerjajmo časovna poteka napetosti izvora in padca napetosti na R2 .
- Obliki časovnih potekov napetosti izvora in padca napetosti na uporu sta sinusni – enaki.
- Padec napetosti na uporu je v fazi z napetostjo izvora.
Prek padca napetosti na ohmski upornosti posredno opazujemo tudi časovni potek toka. Iz do sedaj spoznanih dejstev o električnem toku namreč vemo, da je tok skozi konstantno ohmsko upornost premo sorazmeren z napetostjo:
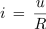
Prepričali se bomo, da plastne upore, kot sta upora v poskusu 3.1.2, lahko pri nizki frekvenci obravnavamo kot upora s praktično čisto ohmsko upornostjo (idealna upora). Zato lahko sklepamo:
- Sinusna izmenična napetost požene v električnem krogu s čisto ohmsko upornostjo sinusni izmenični tok, ki je v fazi z napetostjo.
Velja tudi obratno:
Obe ugotovitvi nazorno prikazuje slika 3.1.4.
O ugotovitvi se lahko prepričamo tudi po matematični poti. V Ohmov zakon za trenutno vrednost toka
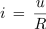
vstavimo izraz za trenutno vrednost sinusne napetost u = Um ∙ sin (ωt):
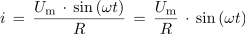

Primerjava izrazov trenutnih vrednosti sinusne napetosti in toka potrjuje identičnost in sočasnost časovnih potekov obeh količin v ohmskem izmeničnem krogu.
| | 3.1.1.3 Energija in moč v ohmskem izmeničnem krogu |