7.1 Idealizirani nihajni krog

Iz e-ELEKTROTEHNIKA plus

Redakcija: 15:34, 12. maj 2010

Poskus 7.1.1

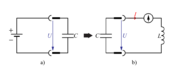
Napolnimo kondenzator kapacitivnosti 470 μF z izvorom enosmerne napetosti 3 V (sl. 7.1.1 a). Napolnjen kondenzator priključimo prek analognega mA-metra z ničelnim položajem kazalca na sredini skale, na tuljavo z lameliranim Fe jedrom in induktivnostjo 65 H (sl. 7.1.1 b).

Slika 7.1.1: Merjenje toka v nihajnem krogu

• Kazalec mA-metra zaniha s frekvenco približno 1 Hz okrog ničelnega položaja.
• Zaradi izgub energije v električnem krogu z realnimi elementi se kazalec po nekaj nihajih umiri.

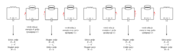
Poskus 7.1.1 smo realizirali z realnima elementoma, kar je povzročilo izgube in hitro iznihavanje energije. Zaradi lažjega razumevanja fizikalnega principa nihanja energije v LC krogu pa vsaj na miselni ravni obravnavani LC krog idealizirajmo. S preklopom naelektrenega kondenzatorja na tuljavo v trenutku to (sl. 7.1.2), smo v kondenzatorju ujeto energijo »sprostili« v krogu s tuljavo.

Slika 7.1.2a: Pretakanje energije v krogu z idealiziranim kondenzatorjem in tuljavo

Slika 7.1.2b: Pretakanje energije v krogu z idealiziranim kondenzatorjem in tuljavo

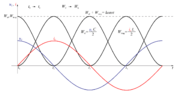
Napetost kondenzatorja bo v času t₀ do t₁ povzročala tok skozi tuljavo. Zaradi napetosti lastne indukcije v tuljavi tok skozi tuljavo narašča postopoma oziroma zaostaja za napetostjo po že znanih pravilih. Energija električnega polja kondenzatorja usiha in se z naraščajočim tokom pojavlja v nastajajočem magnetnem polju tuljave.

Tok praznjenja kondenzatorja doseže največjo vrednost I_m v trenutku izpraznitve kondenzatorja (W_C = 0), to je v trenutku t₁. V trenutku t₁ je celotna energija električnega polja kondenzatorja prešla v energijo magnetnega polja tuljave.

Od trenutka t₁ naprej energija električnega polja kondenzatorja ni več vzrok toka v krogu, zato pa v času t₁ do t₂ skrbi za njegovo vzdrževanje v isti smeri energija magnetnega polja. Tako kot se je napetost lastne indukcije tuljave v času to do t₁ upirala naraščanju toka, se v času t₁ do t₂ upira njegovemu usihanju. Z vzdrževanjem toka v času po t₁ se kondenzator začne polniti v obratni smeri, energija za vzdrževanje toka pa se črpa iz magnetnega polja tuljave.

Ko energija magnetnega polja usahne (t₂), tudi toka v krogu ni več. Kondenzator je prej oddano energijo v celoti dobil nazaj in na njem je ponovno napetost U, le z obrnjeno polariteto.

Od trenutka t₂ naprej je energija električnega polja kondenzatorja ponovno vzrok toka v krogu, toda sedaj zaradi nasprotne polarizacije kondenzatorja tok teče v obratni smeri. Ker se pojav naprej periodično ponavlja, lahko ugotovimo:

Zaradi ugotovljenega imenujemo krog s kondenzatorjem in tuljavo električni nihajni krog, samostojno nihanje energije v krogu pa lastno nihanje, frekvenco lastnega nihanja pa lastna frekvenca. Ker je za tovrstno nihanje potrebna kombinacija kapacitivnosti in induktivnosti, bomo v nadaljevanju uporabljali tudi naziv LC nihajni krog. Opisano lastno nihanje energije je naravni fizikalni pojav, zato velja:

7 Resonančni pojavi

7.2 Lastno nihanje v realnem nihajnem krogu