Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| Vrstica 1: | Vrstica 1: | ||
| - | [[Image:OET2 a poglavje 09 slika 03.svg|thumb|Konjugirani števili <latex>a(\alpha)</latex> in <latex>a(-\alpha)</latex> ležita na enotini krožnici polmera 1.]] [[Image:OET2 a poglavje 09 slika 04.svg|thumb|Konjugirani števili ležita v II. in III. kvadrantu; razlikujeta se le v imaginarnem delu, imata pa enaki absolutni vrednosti.]] Za potrebe analize harmonično vzbujanih vezij vpeljemo določene ''kompleksne količine''«; te so (zgolj in le simbolično) pridružene pravim, električnim količinam: napetosti, toku, moči | + | [[Image:OET2 a poglavje 09 slika 03.svg|thumb|Konjugirani števili <latex>a(\alpha)</latex> in <latex>a(-\alpha)</latex> ležita na enotini krožnici polmera 1.]] [[Image:OET2 a poglavje 09 slika 04.svg|thumb|Konjugirani števili ležita v II. in III. kvadrantu; razlikujeta se le v imaginarnem delu, imata pa enaki absolutni vrednosti.]] Za potrebe analize harmonično vzbujanih vezij vpeljemo določene ''kompleksne količine''«; te so (zgolj in le simbolično) pridružene pravim, električnim količinam: napetosti, toku, moči ... Najprej pa izpostavimo določene uveljavljene dogovore. |
| Vrstica 13: | Vrstica 13: | ||
| - | Njegova absolutna vrednost (označujemo jo tudi z nepodčrtano črko) je | + | Njegova absolutna vrednost (označujemo jo tudi z nepodčrtano črko) je: |
Redakcija: 12:19, 20. maj 2010
Slika:OET2 a poglavje 09 slika 03.svg
Konjugirani števili 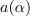 in
in 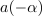 ležita na enotini krožnici polmera 1.
ležita na enotini krožnici polmera 1.
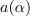
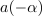
Slika:OET2 a poglavje 09 slika 04.svg
Konjugirani števili ležita v II. in III. kvadrantu; razlikujeta se le v imaginarnem delu, imata pa enaki absolutni vrednosti.

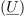
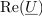
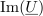
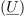
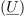
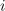
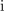
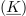
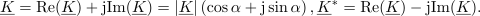
Njegova absolutna vrednost (označujemo jo tudi z nepodčrtano črko) je:
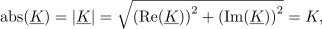
argument pa določa sestavljen izraz:
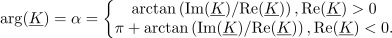
Opombe
- ↑ Osi označujemo tudi z Re in Im, ali realna os in imaginarna os; stvar izbire.
| | 1.3.2 Kazalec harmonične količine |
