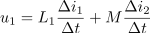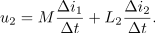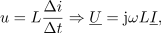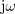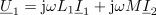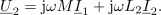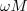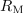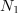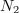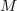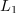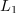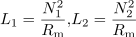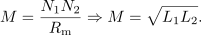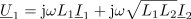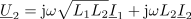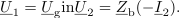|
|
| Vrstica 42: |
Vrstica 42: |
| | | | |
| | | | |
| - | == Prestavno razmerje ==
| + | <references /> |
| | | | |
| - | Prvo značilnost transformatorja dobimo, ko med seboj delimo kazalca napetosti navitij in upoštevamo izraze za induktivnosti:
| |
| - |
| |
| - |
| |
| - | <latex>\frac{ {\underline U _{\mathrm{1} } } }{ {\underline U _{\mathrm{2} } } } = \frac{ { {\mathrm{j} }\omega L_1 \underline I _1 + {\mathrm{j} }\omega \sqrt {L_1 L_2 } \underline I _2 } }{ { {\mathrm{j} }\omega \sqrt {L_1 L_2 } \underline I _1 + {\mathrm{j} }\omega L_2 \underline I _2 } } = \frac{ { {\mathrm{j} }\omega \sqrt {L_1 } } }{ { {\mathrm{j} }\omega \sqrt {L_2 } } } \cdot \frac{ { {\mathrm{j} }\omega \sqrt {L_1 } \underline I _1 + {\mathrm{j} }\omega \sqrt {L_2 } \underline I _2 } }{ { {\mathrm{j} }\omega \sqrt {L_1 } \underline I _1 + {\mathrm{j} }\omega \sqrt {L_2 } \underline I _2 } } = \sqrt {\frac{ {L_1 } }{ {L_2 } } } = \frac{ {N_1 } }{ {N_2 } }.</latex>
| |
| - |
| |
| - |
| |
| - | Verjetno preseneča dejstvo, da sta kazalca napetosti navitj v razmerju števila ovojev (zgolj to in nič več):
| |
| - |
| |
| - |
| |
| - | <latex>{\frac{ {\underline U _{\mathrm{1} } } }{ {\underline U _{\mathrm{2} } } } = \frac{ {N_1 } }{ {N_2 } } = n,}</latex>
| |
| - |
| |
| - |
| |
| - | Število ''n'' je ''prestavno razmerje''. Primer. Razmerje med števili ovojev navitij transformatorja naj bo pet. Ob priključitvi enega od njih na omrežno napetost efektivne vrednosti 230 V bi med sponkama drugega navitja mogli izmeriti napetost efektivne vrednosti 230 V / 5 = 46 V ali pa 230 V × 5 = 1150 V; odvisno od tega, katero od navitij bi bilo primarno.
| |
| - |
| |
| - |
| |
| - | == Sekundarni tok ==
| |
| - |
| |
| - | Če je temu tako, potem sta v enakem razmerju tudi kazalca napetosti vira in napetosti bremena, iz česar sledi izraz za kazalec toka skozi breme:
| |
| - |
| |
| - |
| |
| - | <latex>n = \frac{ {\underline U _{\mathrm{1} } } }{ {\underline U _{\mathrm{2} } } } = \frac{ {\underline U _{\mathrm{g} } } }{ {\underline U _{\mathrm{2} } } }{\mathrm{ } } \Rightarrow {\mathrm{ } }\underline U _{\mathrm{2} } = \frac{ {\underline U _{\mathrm{g} } } }{n}{\mathrm{ } } \Rightarrow {\mathrm{ (} } - \underline I _2 ) = \frac{ {\underline U _{\mathrm{2} } } }{ {\underline Z _{\mathrm{b} } } } = \frac{ {\underline U _{\mathrm{g} } } }{ {n\underline Z _{\mathrm{b} } } }.</latex>
| |
| - |
| |
| - |
| |
| - | Preseneča, da je tok bremena povsem neodvisen od reaktanc transformatorja.
| |
| - |
| |
| - |
| |
| - | == Primarni tok ==
| |
| - |
| |
| - | Iz napetostne enačbe drugega navitja izrazimo primarni tok. Ko vanj vpletemo še prestavo, dobimo:
| |
| - |
| |
| - |
| |
| - | <latex>\underline U _{\mathrm{2} } = {\mathrm{j} }\omega \sqrt {L_1 L_2 } \underline I _1 + {\mathrm{j} }\omega L_2 \underline I _2 {\mathrm{ } } \Rightarrow {\mathrm{ } }\underline I _1 = \frac{ {\underline U _{\mathrm{2} } } }{ { {\mathrm{j} }\omega \sqrt {L_1 L_2 } } } - \sqrt {\frac{ {L_2 } }{ {L_1 } } } \underline I _2 = \frac{ {\underline U _{\mathrm{1} } } }{ { {\mathrm{j} }\omega L_1 } } + \frac{ {( - \underline I _2 )} }{n}.</latex>
| |
| - |
| |
| - |
| |
| - | Kaj vidimo? Primarni tok oblikuje vsota dveh sumandov: prvega določata kazalec napetosti in impedanca primarja, drugega pa kazalec toka v bremenu. V nadaljevanju bomo spoznali, da ima vsak od njiju določen fizikalni pomen.
| |
| - |
| |
| - |
| |
| - | == Magnetilni in ravnotežni tok ==
| |
| - |
| |
| - | Jedro transformatorja vzbujata dve magnetni napetosti (''N''<sub>1</sub><u>''I''</u><sub>1</sub> in ''N''<sub>2</sub><u>''I''</u><sub>2</sub>); glede na oznaki tokov (<u>''I''</u><sub>1</sub> in <u>''I''</u><sub>2</sub>) skozi navitji (v piki) se magnetni napetosti podpirata. Kazalec rezultančne magnetne napetosti,
| |
| - |
| |
| - |
| |
| - | <latex>N_1 \underline I _1 + N_2 \underline I _2 = N_1 \left( {\frac{ {\underline U _{\mathrm{1} } } }{ { {\mathrm{j} }\omega L_1 } } - \frac{ {\underline I _2 } }{n} } \right) + N_2 \underline I _2 = N_1 \frac{ {\underline U _{\mathrm{1} } } }{ { {\mathrm{j} }\omega L_1 } }\underbrace{ - N_1 n^{ - 1} \underline I _2 + N_2 \underline I _2 }_0 = N_1 \frac{ {\underline U _{\mathrm{1} } } }{ { {\mathrm{j} }\omega L_1 } },</latex>
| |
| - |
| |
| - |
| |
| - | je povsem neodvisen od sekundarnega toka, sicer pa tolikšen, kot da bi jedro magnetil le prvi del primarnega toka, magnetna napetost drugega dela toka pa bi pri tem zgolj držala ravnotežje z magnetno napetostjo sekundarnega toka; to dvoje je razlog, da prvi del primarnega toka imenujemo ''magnetilni tok'' <u>''I''</u><sub>1m</sub>, drugega pa ''ravnotežni tok'' (<u>''I''</u><sub>1r</sub>):
| |
| - |
| |
| - |
| |
| - | <latex>{\underline I _{1{\mathrm{m} } } = \frac{ {\underline U _{\mathrm{1} } } }{ { {\mathrm{j} }\omega L_1 } }}</latex> in <latex>{\underline I _{ {\mathrm{1r} } } = - \frac{ {\underline I _2 } }{n} = - \frac{ {N_2 } }{ {N_1 } }\underline I _2 {\mathrm{ } } \Rightarrow {\mathrm{ } }\underline I _1 = \underline I _{1{\mathrm{m} } } + \underline I _{ {\mathrm{1r} } } .}</latex>
| |
| - |
| |
| - |
| |
| - | == Kazalčni diagram vezja ==
| |
| - | [[Slika:OET2_a_poglavje_52_slika_04.svg|thumb|Kazalčni diagram tokov in napetosti transformatorja. ]]
| |
| - | Ugotovitve še najlepše povzame kazalčni diagram (slika 4). Risanje se odvija takole: izberemo lego kazalca <u>''U''</u><sub>1</sub>; n = 2, kazalec ''<u>U</u>''<sub>2</sub> je sofazen kazalcu <u>''U''</u><sub>1</sub>, kazalec toka <u>''I''</u><sub>1m</sub> zaostaja za ''<u>U</u>''<sub>1</sub> za 90 °, <u>''Z''</u><sub>b</sub> naj bo induktivnega značaja, kazalec toka (–<u>''I''</u><sub>2</sub>) zaostaja za kot <latex>\phi</latex> za ''<u>U</u>''<sub>2</sub>, kazalec ravnotežnega toka <u>''I''</u><sub>1r</sub> je sofazen z (–''<u>I</u>''<sub>2</sub>), kazalec toka <u>''I''</u><sub>1</sub> je enak vsoti kazalcev ''<u>I</u>''<sub>1m</sub> in <u>''I''</u><sub>1r</sub>. To je vse.
| |
| - |
| |
| - |
| |
| - | == Moči transformatorja ==
| |
| - |
| |
| - | [[Slika:OET2_a_poglavje_52_slika_05.svg|thumb|Kazalčni diagram moči transformacije. ]]
| |
| - | Vhodno kompleksno moč <u>''S''</u><sub>1</sub> (moč v transformator) določata kazalca primarne napetosti in toka; glede na izpisane relacije sledi:
| |
| - |
| |
| - |
| |
| - | <latex>\underline S _1 = {\textstyle{\frac{1}{2} } }\underline U _{\mathrm{1} } (\underline I _1 )* = {\textstyle{\frac{1}{2} } }\underline U _{\mathrm{1} } \left( {\underline I _{1{\mathrm{m} } } - \underline I _2 /n} \right)* = {\textstyle{\frac{1}{2} } }\underline U _{\mathrm{1} } (\underline I _{1{\mathrm{m} } } )* + {\textstyle{\frac{1}{2} } }n\underline U _{\mathrm{2} } n^{ - 1} ( - \underline I _2 )* = </latex>
| |
| - |
| |
| - |
| |
| - | <latex>{\textstyle{\frac{1}{2} } }\underline U _{\mathrm{1} } (\underline I _{1{\mathrm{m} } } )* + {\textstyle{\frac{1}{2} } }\underline U _{\mathrm{2} } ( - \underline I _2 )*.</latex>
| |
| - |
| |
| - |
| |
| - | Vhodna kompleksna moč je enak vsoti dveh: v prvi prepoznamo imaginarno moč magnetenja jedra (j<latex>Q</latex><sub>1m</sub>), v drugi pa kompleksno moč bremena (<u>''S''</u><sub>b</sub>):
| |
| - |
| |
| - |
| |
| - | <latex>{\underline S _1 = {\mathrm{j} }Q_{ {\mathrm{1m} } } + \underline S _{\mathrm{b} } {\mathrm{ } } \Rightarrow {\mathrm{ } }P_1 = P_{\mathrm{b} }}</latex> in <latex>{Q_1 = Q_{ {\mathrm{1m} } } + Q_{\mathrm{b} } .}</latex>
| |
| - |
| |
| - |
| |
| - | Vhodna delovna moč je enaka delovni moči bremena, vhodna jalova moč pa je za jalovo moč magnetenja jedra večja kot jalova moč bremena (slika 5).
| |
| - |
| |
| - |
| |
| - | == Transformacije ==
| |
| - |
| |
| - | Ustavimo se ob transformacijah oziroma pretvorbah, ki jih ponuja transformator.
| |
| - |
| |
| - |
| |
| - | 1) Prva je zajeta v prestavnem razmerju ''n'' = ''N''<sub>1</sub> / ''N''<sub>2</sub>: v tem, da zmore transformator harmonično napetost z nižjega pretvoriti na višji nivo in obratno. Ta možnost je resnično dobrodošla in jo pogosto koristimo. Primer. Na voljo imamo omrežno (sinusno) napetost, ampak nam nivo 230 V ne ustreza; želimo višjo (ali nižjo) napetost za napajanje naprave. Nič lažjega: med omrežje in breme vežemo transformator, ki ima primerno razmerje n in težava je rešena.
| |
| - |
| |
| - |
| |
| - | 2) Drugo pretvorbo transformatorja zasledimo v relacijah med kazalci tokov in delnih tokov v navitjih:
| |
| - |
| |
| - |
| |
| - | <latex>\underline I _1 = \frac{ {\underline U _{\mathrm{1} } } }{ { {\mathrm{j} }\omega L_1 } } + \frac{ {( - \underline I _2 )} }{n} = \underline I _{1{\mathrm{m} } } + \underline I _{1{\mathrm{r} } } {\mathrm{ } } \Rightarrow {\mathrm{ } }\frac{ {\underline I _2 } }{ {\underline I _{1{\mathrm{r} } } } } = - n = - \frac{ {N_1 } }{ {N_2 } }.</latex>
| |
| - |
| |
| - |
| |
| - | Tudi razmerje kazalcev ravnotežnega in sekundarnega toka določa prestavno razmerje, in sicer, da navitju z večjim številom ovojev pripada manjši tok, in obratno, in da sta si ta toka (zaradi minusa) protifazna.
| |
| - |
| |
| - |
| |
| - | 3) Tretja pretvorba se dotika tako kompleksnih moči kot kazalca primarnega toka:
| |
| - |
| |
| - |
| |
| - | <latex>\underline S _1 = {\textstyle{\frac{1}{2} } }\underline U _{\mathrm{1} } (\underline I _1 )* = {\textstyle{\frac{1}{2} } }\underline U _{\mathrm{1} } \left( {\underline I _{1{\mathrm{m} } } - \underline I _2 /n} \right)* = {\mathrm{j} }Q_{ {\mathrm{1m} } } + \underline S _{\mathrm{b} } .</latex>
| |
| - |
| |
| - |
| |
| - | Razmerje med imaginarno močjo magnetenja in kompleksno močjo bremena je enako razmerju med kazalcem magnetilnega in kazalcem ravnotežnega toka. Pri projektiranju transformatorja stremimo, da je razmerje čim manjše,
| |
| - |
| |
| - |
| |
| - | <latex>\left| { {\mathrm{j} }Q_{ {\mathrm{1m} } } } \right| \ll \left| {\underline S _{\mathrm{b} } } \right|{\mathrm{ } } \Rightarrow {\mathrm{ } }\left| {\underline I _{1{\mathrm{m} } } } \right| \ll \left| { - \underline I _2 /n} \right|{\mathrm{ } } \Rightarrow {\mathrm{ } }\left| {\frac{ {\underline U _{\mathrm{1} } } }{ { {\mathrm{j} }\omega L_1 } } } \right| \ll \left| { - \underline I _2 /n} \right| = \left| {\frac{ {\underline U _{\mathrm{2} } } }{ {n\underline Z _{\mathrm{b} } } } } \right| = \left| {\frac{ {\underline U _{\mathrm{1} } } }{ {n^2 \underline Z _{\mathrm{b} } } } } \right|,</latex>
| |
| - |
| |
| - |
| |
| - | da je delež magnetilnega v primarnem toku čim manjši.<ref>V normalnem obratovanju transformatorja naj bi bila absolutna vrednost magnetilnega toka manjša od odstotka absolutne vrednosti primarnega toka.</ref> To dosežmo, ko je
| |
| - |
| |
| - |
| |
| - | <latex>\left| {\underline U _{\mathrm{1} } /{\mathrm{j} }\omega L_1 } \right| \ll \left| {\underline U _{\mathrm{1} } /n^2 \underline Z _{\mathrm{b} } } \right|{\mathrm{ } } \Rightarrow {\mathrm{ } }\left| {\underline Z _{\mathrm{b} } } \right| \ll \left| { {\mathrm{j} }\omega L_1 /n^2 } \right| = \left| { {\mathrm{j} }\omega L_2 } \right|,</latex>
| |
| - |
| |
| - |
| |
| - | oziroma ko reaktanca sekundarnega navitja zelo preseže absolutno vrednost impedance bremena. Če to dosežemo, velja naslednje:
| |
| - |
| |
| - |
| |
| - | <latex>\left| {\underline I _{1{\mathrm{m} } } } \right| \ll \left| { - \underline I _2 /n} \right|{\mathrm{ } } \Rightarrow {\mathrm{ } }\underline I _1 \cong - n^{ - 1} \underline I _2 {\mathrm{ in } }\underline S _1 \cong \underline S _{\mathrm{b} } .</latex>
| |
| - |
| |
| - |
| |
| - | 4) Četrta pretvorba je pretvorba impedance bremena v vhodno impedanco. Če magnetilni tok zanemarimo, potem je impedanca navideznega bremena enaka kvocientu kazalca napetosti vira in kazalca primarnega toka:
| |
| - |
| |
| - |
| |
| - | <latex>{\underline Z _1 = \frac{ {\underline U _1 } }{ {\underline I _1 } } \cong \frac{ {n\underline U _2 } }{ { - \underline I _2 /n} } = n^2 \frac{ {\underline U _2 } }{ {( - \underline I _2 )} } = n^2 \underline Z _{\mathrm{b} } .}</latex>
| |
| - |
| |
| - |
| |
| - | Transformator torej transformira tudi impedanco bremena. Pri prestavi pet in bremenski impedanci (2 – j3) <latex>\Omega</latex> je vrednost impedance navideznega bremena (50 – j75) <latex>\Omega</latex>. Ta možnost je aktualna v elektroniki.
| |
| - |
| |
| - |
| |
| - | == Idealni transformator ==
| |
| - |
| |
| - | [[Slika:OET2_a_poglavje_52_slika_06.svg|thumb|Označevanje simbola idealnega transformatorja. ]]
| |
| - | Obravnavani transformator je bil idealiziran, brez izgub in popolno sklopljenih navitij, idealni pa bi bil tisti, katerega jedro bi imelo neskončno permeabilnost (''R''m = 0) oziroma neskončne induktivnosti, da bi bila nična tako magnetilni tok kot moč za magnetenje jedra. Podatek idealnega transformatorja sta v tem primeru števili ''N''<sub>1</sub> in ''N''<sub>2</sub> oziroma razmerje ''n''. Električni simbol idealnega transformatorja je identičen prejšnjemu, le da impedance smiselno zamenjata števili ovojev (slika 6). Njegovi enačbi sta v resnici le dve, napetostna in tokovna:
| |
| - |
| |
| - |
| |
| - | <latex>{\frac{ {\underline U _{\mathrm{1} } } }{ {\underline U _{\mathrm{2} } } } = \frac{ {N_1 } }{ {N_2 } } = n}</latex> in <latex>{\frac{ {\underline I _{\mathrm{1} } } }{ {\underline I _2 } } = - \frac{ {N_2 } }{ {N_1 } } = - n^{ - 1} .}</latex>
| |
| - |
| |
| - |
| |
| - | Razmerje napetosti določa prestavno razmerje, razmerje protifaznih tokov pa recipročna vrednost prestavnega razmerja. Ko idealni transformator povezuje breme z virom, veljata še enačbi:<ref>S pomočjo idealnega transformatorja moremo oblikovati še drugačno nadomestno vezje brezizgubnega transformatorja: vzporedno k primarnemu navitju idealnega transformatorja pridružimo tuljavo z induktivnostjo primarnega navitja. Primarni tok se v tem primeru deli v magnetilni skozi tuljavo in v ravnotežni skozi primar idealnega transformatorja (torej v smislu izraza za primarni tok).</ref>
| |
| - |
| |
| - |
| |
| - | <latex>{\underline S _1 = \underline S _{\mathrm{b} }}</latex> in <latex>{\underline Z _1 = n^2 \underline Z _{\mathrm{b} } ,}</latex>
| |
| - |
| |
| - |
| |
| - | da sta vhodni in izhodni kompleksni moči enaki in da se impedanca bremena transformira na vhod s kvadratom prestave.
| |
| - |
| |
| - |
| |
| - | == Uporaba transformatorja ==
| |
| - |
| |
| - | Transformator zmore vhodno energijo praktično v celoti prenesti na sekundarno stran; pri tem med primarjem in sekundarjem zamenja nivo napetosti v razmerju prestave (''n''), nivo toka pa v razmerju (''n''<sup>–1</sup>). Brez te možnosti, ki jo ponuja transformator, bi bil prenos električne energije na daljavo zelo drag. Zakaj? Inducirane napetosti sinhronskih generatorjev v elektrarnah so velikosti kV. Pri moči 300 MW bi morali biti preseki daljnovodnih žic debeline (dm)<sup>2</sup>, česar ne bi prenesli niti stebri in še manj ekonomija. Odgovor je tu: na strani generatorja je potrebno postaviti transformator, ki kV napetost pretvori na 100 kV, 100 kA tok pa na nivo kA, potrebne daljnovodne vrvi so zaradi tega tanjše, lažje in cenejše. Na strani porabnikov je potrebno zadevo ponoviti v nasprotno smer: od višje k nižji napetosti.
| |
| - |
| |
| - |
| |
| - | <references />
| |
| | | | |
| | {{Hierarchy footer}} | | {{Hierarchy footer}} |
Transformator je naprava, ki ima nekaj lepih električnih lastnosti; zaradi njih ni nepogrešljiv le pri distribuciji električne energije, ampak tudi v elektroniki. Zasnovo transformatorja smo predstavili v okviru magnetnih vezjih, njegovo idealizirano nadomestno vezje in ustrezni enačbi pa v okviru sklopljenih tuljav. Modela brezizgubnega transformatorja se bomo v nadaljevanju tudi oprijeli in poskušali iz njega prepoznati lastnosti, ki transformator odlikujejo (slika 1).[1]
razkriva podobnost med časovnim in kompleksnim zapisom: napetost preide v kazalec napetosti, hitrost spreminjanja toka pa v kazalec toka, multipliciran z
(induktivnost je le multiplikator). Kar velja zanjo, mora smiselno veljati tudi za enačbo z več podobnimi sumandi. Če je tako, potem sta:
V modelnem vezju spremenimo temu ustrezno tudi oznake: toka in napetosti zamenjajo njihovi kazalci, induktivnosti nadomestijo z j množene reaktance in
navitij, piki zadržita svoj pomen (slika 2). Nič kaj drugače ni pri transformatorju oziroma popolnem sklopu dveh navitij na visokopermeabilnem jedru. V enačbi kaže vplesti preproščino, da so izrazi za induktivnosti podobni in določeni z magnetno upornostjo jedra (