1.3.7 Eulerjeva formula

Iz e-ELEKTROTEHNIKA plus

Na splošnosti nič ne izgubimo, če se za hip omejimo na kompleksno število, ki leži na krožnici polmera 1. Slaven nemški matematik Leonhard Euler je prišel do ugotovitve, da se dá kompleksno število zapisati tudi v eksponentni obliki:

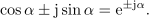
Enačbo moremo preveriti. Naj ta velja. Če množimo dve kompleksni števili in upoštevamo pravila za množenje potenc, sledi zveza, ki jo že poznamo:

Z Eulerjevo formulo moremo kazalec zapisati morda še bolj pregledno:

Kazalca in sta dana v eksponentni obliki; njun produkt in kvocient sta:

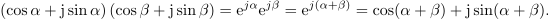
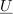
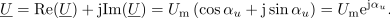
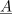
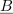
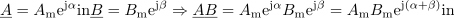
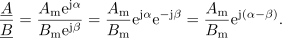
Kaj je prednost Eulerjeve formule? Izkazuje jo pri deljenju (množenju), ni pa uporabna pri seštevanju (odštevanju) kompleksnih števil.

Zgled 4.

Opravimo produkt in kvocient kazalcev 2 in na dva načina! ⇒

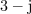
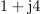
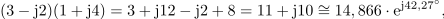
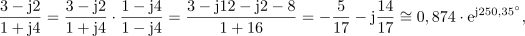
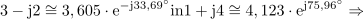
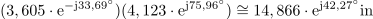
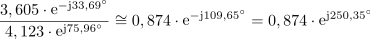
Kaj je sporočilo? Če sta kazalca podana v komponentni obliki, potem ju v tej obliki lahko tudi množimo in delimo, če pa sta dana v eksponentni obliki, ju v tej obliki enostavno delimo ali množimo, za seštevanje ali odštevanje pa ju moramo predhodno pač pretvoriti v komponentno obliko.

1.3.6 Množenje in deljenje z »j«

2 Lastnost in zakonitosti izmeničnih krogov (višji nivo)