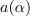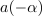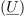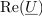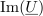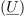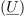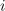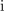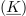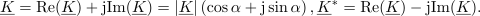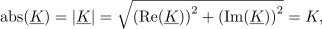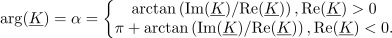Iz e-ELEKTROTEHNIKA plus
Za potrebe analize harmonično vzbujanih vezij vpeljemo določene
kompleksne količine«; te so (zgolj in le simbolično) pridružene pravim, električnim količinam: napetosti, toku, moči ... Najprej pa izpostavimo določene uveljavljene dogovore.
Simbol (črko) kompleksne količine podčrtujemo (to naredi razviden razloček med fizikalno in njej prirejeno kompleksno količino). Če je črka
simbol za napetost, potem je znak
simbol za njej pridruženo »kompleksno napetost«, katere realni del je
, imaginarni del pa je
. Čeravno je pri tem
zgolj kompleksno število, izraženo v voltih, ga v kompleksni ravnini zaradi nazornosti upodabljamo z daljico od izhodišča do točke
, ki jo opremimo še s strelico _ da postane kvazi-vektor; rečemo mu
kazalec napetosti.
Za imaginarno enoto ne uporabljamo črke i (kot je to ustaljeno v matematiki), ampak j; razlog je v tem, da s (sicer
ležečo) črko
označujemo tudi električni tok. Črka
bi torej (formalno) nič ne motila; ali pač! Zaradi teh dopolnitev ter zamenjav, in iz razloga, da upodabljamo v Gaussovi ravnini kazalce različnih količin, bomo osi ravnine označevali zgolj z znakoma (1) in (j) (slika 5).
[1]
Dogovore povzemajo zapisi, ki se naslavlajo na nek splošen kazalec
:
Njegova absolutna vrednost (označujemo jo tudi z nepodčrtano črko) je:
argument pa določa sestavljen izraz:
Opombe
- ↑ Osi označujemo tudi z Re in Im, ali realna os in imaginarna os; stvar izbire.
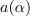 in
in 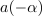 ležita na enotini krožnici polmera 1.
ležita na enotini krožnici polmera 1.