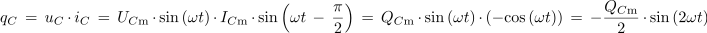Iz e-ELEKTROTEHNIKA plus
V kapacitivnem izmeničnem krogu označujemo trenutno moč s qC, določena pa je s produktom trenutnih vrednosti napetosti in toka:
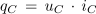
Iz časovnih potekov napetosti in toka v kapacitivnem izmeničnem krogu (sl. 3.1.18) dobimo na že znani način časovni potek moči (sl. 3.1.22):
- Časovni potek moči sinusnega izmeničnega toka ima v kapacitivnem izmeničnem krogu sinusno obliko z dvojno frekvenco[1] toka.
Pozitivna površina, ki jo v tem primeru oklene krivulja moči s časovno osjo v ¼ periode, predstavlja električno energijo, ki je v omenjeni četrtinki periode pritekla iz generatorja in se nakopičila v električnem polju[2] kondenzatorja.
Zaradi enakosti pozitivne in negativne površine se, podobno kot pri tuljavi, v naslednji četrtinki periode z usihanjem električnega polja v kondenzatorju (slika 3.1.29) nakopičena energija v celoti vrne v generator.
- Na kondenzatorju se, podobno kot na tuljavi, električna energija ne pretvarja v energijo drugih oblik in se ne sprošča iz električnega kroga.
- Energija se v kapacitivnem izmeničnem krogu brez učinka (jalovo), z dvojno frekvenco toka, le preliva iz generatorja v kondenzator in obratno. Imenujemo jo jalova energija.
Iz ugotovljenih razlogov imenujemo kapacitivno upornost jalova upornost, tok v kapacitivnem izmeničnem krogu jalovi tok in moč toka v kapacitivnem izmeničnem krogu jalova moč (QC).
- V primeru faznega kota φ = - 90 ° je v izmeničnem krogu prisotna le jalova moč.
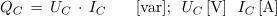
ali tudi
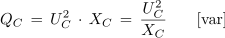
Moč izmeničnega toka v kapacitivnem krogu merimo enako kot v induktivnem krogu v varih.
Opombe
| | 3.2 Vezave upora, tuljave in kondenzatorja |