2.5.2 Jalova ali reaktivna moč

Iz e-ELEKTROTEHNIKA plus

Redakcija: 16:09, 14. maj 2010 (view source) Admin (Pogovor | prispevki) m (1 revision) ← Starejša redakcija		Trenutna redakcija s časom 17:43, 12. julij 2010 (view source) Admin (Pogovor | prispevki)
(One intermediate revision not shown)
Vrstica 1:		Vrstica 1:
-	[[Image:OET2 a poglavje 32 slika 43-2.svg|thumb|Časovni diagrami treh moči: nenegativne moči <latex>p_1</latex>, harmonične moči <latex>p_2</latex> in moči <latex>p</latex> bremena.]] Poprečna moč pa žal ne da celovitega vpogleda v močnostne razmere v bremenu. Uvodoma smo opozorili na del energije, ki se v času negativne moči vrača viru, da se v resnici izmenjuje med bremenom in virom. Potrebovali bi torej mero, ki bi govorila o moči te izmenjave. Izhajali bomo iz izraza za moč bremena. 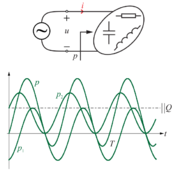Preoblikujmo ga na tale način:	+	[[Image:eele_slika_visji_042.svg|thumb|Slika 42: Časovni diagrami treh moči: nenegativne moči <latex>p_1</latex>, harmonične moči <latex>p_2</latex> in moči <latex>p</latex> bremena.]] Poprečna moč pa, žal, ne da celovitega vpogleda v močnostne razmere v bremenu. Uvodoma smo opozorili na del energije, ki se v času negativne moči vrača viru, da se v resnici izmenjuje med bremenom in virom. Potrebovali bi torej mero, ki bi govorila o moči te izmenjave. Izhajali bomo iz izraza za moč bremena. Preoblikujmo ga na tale način:
Vrstica 11:		Vrstica 11:
-	Moč <latex>p</latex> se tudi tokrat izraža z vsoto dveh: moči <latex>p_1</latex>, ki je vseskozi nenegativna in spominja na moč sproščanja toplote v uporu, ter moči <latex>p_2</latex>, ki je harmonična in spominja na moč polnjenja kondenzatorja ali tuljave (slika 2). Za moč izmenjave energije med virom in bremenom je potemtakem odgovorna moč <latex>p_2</latex>, katere amplitudo določa izraz	+	Moč <latex>p</latex> se tudi tokrat izraža z vsoto dveh: moči <latex>p_1</latex>, ki je vseskozi nenegativna in spominja na moč sproščanja toplote v uporu, ter moči <latex>p_2</latex>, ki je harmonična, in spominja na moč polnjenja kondenzatorja ali tuljave (slika 42). Za moč izmenjave energije med virom in bremenom je potemtakem odgovorna moč <latex>p_2</latex>, katere amplitudo določa izraz
Vrstica 26:		Vrstica 26:
-	'''Zgled 2.'''	+	'''Zgled 2'''
	Motorju iz prvega zgleda izračunajmo jalovo moč. ⇒ Sklicujemo se na enačbi		Motorju iz prvega zgleda izračunajmo jalovo moč. ⇒ Sklicujemo se na enačbi
Vrstica 46:		Vrstica 46:
-	Podatek o jalovosti bremena je pomemben za distributerja električne energije. Zakaj? Zamislimo si zlobno možnost oziroma slučaj, ko bi se vsi koristniki električne energije dogovorili in na omrežje priključili zgolj kondenzatorje. Daljnovodne vrvi bi zasičevali zgolj polnilni toki (morda bi ti dosegli že nivo nazivnih tokov), števci delovne energije pa bi kazali nično porabo. Nek drug, resen odjemalec električne energije bi bil zaradi te igre odrinjen. Nerodno! Da bi bil učinek jalovosti bremena na omrežje čim manjši, zahteva distributer električne energije od vseh večjih odjemalcev to, da imajo vgrajen tudi števec ''jalove energije'';<ref>Jalova energija je definirana s produktom absolutne vrednosti jalove moči in časa.</ref> da ti to (sprejeto in čeravno vrnjeno) energijo tudi plačajo!	+	Podatek o jalovosti bremena je pomemben za distributerja električne energije. Zakaj? Zamislimo si zlobno možnost oziroma primer, ko bi se vsi koristniki električne energije dogovorili in na omrežje priključili zgolj kondenzatorje. Daljnovodne vrvi bi zasičevali zgolj polnilni toki (morda bi ti dosegli že nivo nazivnih tokov), števci delovne energije pa bi kazali nično porabo. Nek drug, resen odjemalec električne energije bi bil zaradi te igre odrinjen. Nerodno! Da bi bil učinek jalovosti bremena na omrežje čim manjši, zahteva distributer električne energije od vseh večjih odjemalcev to, da imajo vgrajen tudi števec ''jalove energije'';<ref>Jalova energija je definirana s produktom absolutne vrednosti jalove moči in časa.</ref> da ti to (sprejeto in čeravno vrnjeno) energijo tudi plačajo.

---

Trenutna redakcija s časom 17:43, 12. julij 2010

Poprečna moč pa, žal, ne da celovitega vpogleda v močnostne razmere v bremenu. Uvodoma smo opozorili na del energije, ki se v času negativne moči vrača viru, da se v resnici izmenjuje med bremenom in virom. Potrebovali bi torej mero, ki bi govorila o moči te izmenjave. Izhajali bomo iz izraza za moč bremena. Preoblikujmo ga na tale način:

Moč se tudi tokrat izraža z vsoto dveh: moči , ki je vseskozi nenegativna in spominja na moč sproščanja toplote v uporu, ter moči , ki je harmonična, in spominja na moč polnjenja kondenzatorja ali tuljave (slika 42). Za moč izmenjave energije med virom in bremenom je potemtakem odgovorna moč , katere amplitudo določa izraz

ki, zaradi , bremen kapacitivnega značaja žal »ne zna« ločiti od bremen induktivnega značaja. Da se informacija o značaju bremena le ne bi izgubila, je jalova ali reaktivna moč bremena opredeljena takole:

Breme induktivnega značaja () ima reaktivno moč pozitivno, breme kapacitivnega značaja () pa ima jalovo moč negativno; breme, ki ima jalovo moč enako nič (), ima uporovni značaj.

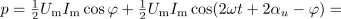
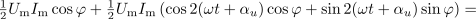
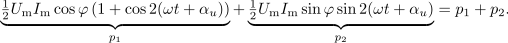
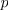
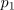
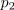
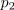
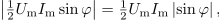
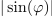
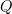
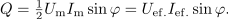
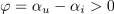
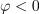
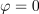
Zgled 2

Motorju iz prvega zgleda izračunajmo jalovo moč. ⇒ Sklicujemo se na enačbi

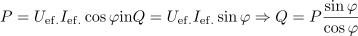
in trigonometrično zvezo

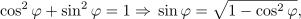
iz česar sledi:

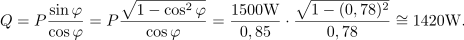
Podatek o jalovosti bremena je pomemben za distributerja električne energije. Zakaj? Zamislimo si zlobno možnost oziroma primer, ko bi se vsi koristniki električne energije dogovorili in na omrežje priključili zgolj kondenzatorje. Daljnovodne vrvi bi zasičevali zgolj polnilni toki (morda bi ti dosegli že nivo nazivnih tokov), števci delovne energije pa bi kazali nično porabo. Nek drug, resen odjemalec električne energije bi bil zaradi te igre odrinjen. Nerodno! Da bi bil učinek jalovosti bremena na omrežje čim manjši, zahteva distributer električne energije od vseh večjih odjemalcev to, da imajo vgrajen tudi števec jalove energije;^[1] da ti to (sprejeto in čeravno vrnjeno) energijo tudi plačajo.

Opombe

1. ↑ Jalova energija je definirana s produktom absolutne vrednosti jalove moči in časa.

2.5.1 Delovna ali aktivna moč

2.5.3 Kompleksna moč