Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
| Vrstica 1: | Vrstica 1: | ||
| - | [[Slika: | + | [[Slika:eele_slika_visji_074.svg|thumb|Slika 74: RLC vezje vzbujata dva harmonična vira.]] |
Če so viri v vezju koherentni (enakih frekvenc), se opravil lotimo z metodami, ki jih poznamo že iz enosmernih vezij. Nekaj več dela nas čaka v primeru nekoherentnih virov. Vezje rešujemo s pomočjo kompleksnega računa in po korakih: prvič, kot da je aktiven le prvi, drugič le drugi vir in tako do zadnjega vira. Delne rešitve pretvorimo zatem v časovne zapise in jih kot takšne tudi seštejemo ter s tem pridobimo končno rešitev za napetosti in toke v vezju. | Če so viri v vezju koherentni (enakih frekvenc), se opravil lotimo z metodami, ki jih poznamo že iz enosmernih vezij. Nekaj več dela nas čaka v primeru nekoherentnih virov. Vezje rešujemo s pomočjo kompleksnega računa in po korakih: prvič, kot da je aktiven le prvi, drugič le drugi vir in tako do zadnjega vira. Delne rešitve pretvorimo zatem v časovne zapise in jih kot takšne tudi seštejemo ter s tem pridobimo končno rešitev za napetosti in toke v vezju. | ||
| Vrstica 5: | Vrstica 5: | ||
'''Zgled 4''' | '''Zgled 4''' | ||
| - | Vezje elementov <latex>R-L-C</latex> s podatki <latex>R=10\,\Omega</latex>, <latex>C=100\,{\mathrm{\mu F}}</latex> in <latex>L=25\,{\mathrm{mH}}</latex> vzbujata vira z napetostma <latex>u_1=10\,{\mathrm{V}}\cdot \cos (400\,{\mathrm{s^{-1}}}\,t)</latex> in <latex>u_2=20\,{\mathrm{V}}\cdot \cos (400\,{\mathrm{s^{-1}}}\,t)</latex> (slika | + | Vezje elementov <latex>R-L-C</latex> s podatki <latex>R=10\,\Omega</latex>, <latex>C=100\,{\mathrm{\mu F}}</latex> in <latex>L=25\,{\mathrm{mH}}</latex> vzbujata vira z napetostma <latex>u_1=10\,{\mathrm{V}}\cdot \cos (400\,{\mathrm{s^{-1}}}\,t)</latex> in <latex>u_2=20\,{\mathrm{V}}\cdot \cos (400\,{\mathrm{s^{-1}}}\,t)</latex> (slika 74). Izračunajmo delovno moč v uporu. ⇒ Kazalca napetosti harmoničnih virov sta: <latex>\underline U _1={\mathrm{10\,V}}</latex> in <latex>\underline U _2={\mathrm{-j10\,V}}</latex>. |
Admitance bremen so: | Admitance bremen so: | ||
Trenutna redakcija s časom 18:45, 12. julij 2010
Če so viri v vezju koherentni (enakih frekvenc), se opravil lotimo z metodami, ki jih poznamo že iz enosmernih vezij. Nekaj več dela nas čaka v primeru nekoherentnih virov. Vezje rešujemo s pomočjo kompleksnega računa in po korakih: prvič, kot da je aktiven le prvi, drugič le drugi vir in tako do zadnjega vira. Delne rešitve pretvorimo zatem v časovne zapise in jih kot takšne tudi seštejemo ter s tem pridobimo končno rešitev za napetosti in toke v vezju.
Zgled 4
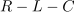
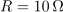
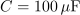
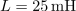
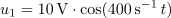
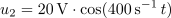
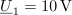
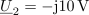
Admitance bremen so:
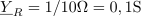
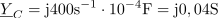
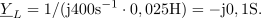
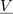
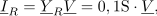
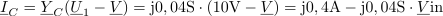
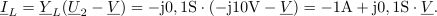
Vsota kazalcev vejnih tokov v tem spojišču je enaka nič:

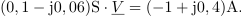
Od tu sledi kazalec potenciala:
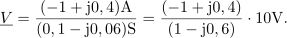
Kazalec moči v uporu je:
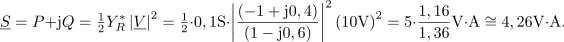
Delovna moč v uporu je 4,26 W, jalova moč pa je (seveda) enaka nič.
| | 3.9 Bilanca moči v izmeničnem vezju |