Iz e-ELEKTROTEHNIKA plus
(Nova stran z vsebino: Slika 3.2.9: Trikotnik napetosti in upornosti zaporednega kroga z uporom, tuljavo in kondenzatorjem Iz sl. 3.2.8 so razvidni trije m…) |
|||
| (7 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| + | <animacija>eele_animacija_006_RLC_vezje_zaporedno_impedance.swf|Upornosti v zaporednem RLC krogu</animacija> | ||
[[Image:eele_slika_3_2_9.svg|thumb|right|Slika 3.2.9: Trikotnik napetosti in upornosti zaporednega kroga z uporom, tuljavo in kondenzatorjem]] | [[Image:eele_slika_3_2_9.svg|thumb|right|Slika 3.2.9: Trikotnik napetosti in upornosti zaporednega kroga z uporom, tuljavo in kondenzatorjem]] | ||
| - | + | [[Image:eele_foto_181.jpg|thumb|right|Fotografija 181]] | |
| + | [[Image:eele_foto_182.jpg|thumb|right|Fotografija 182]] | ||
| + | [[Image:eele_foto_183.jpg|thumb|right|Fotografija 183]] | ||
| + | [[Image:eele_foto_184.jpg|thumb|right|Fotografija 184]] | ||
| + | [[Image:eele_foto_185.jpg|thumb|right|Fotografija 185]] | ||
Iz sl. 3.2.8 so razvidni trije možni splošni primeri značaja izmeničnega kroga z zaporedno vezavo upora, tuljave in kondenzatorja. Iz praktičnih razlogov se za nadaljnjo obravnavo odločimo za vezavo z induktivnim značajem (sl. 3.2.9). | Iz sl. 3.2.8 so razvidni trije možni splošni primeri značaja izmeničnega kroga z zaporedno vezavo upora, tuljave in kondenzatorja. Iz praktičnih razlogov se za nadaljnjo obravnavo odločimo za vezavo z induktivnim značajem (sl. 3.2.9). | ||
| Vrstica 19: | Vrstica 24: | ||
Zaradi enostavnosti bomo pri obravnavi napetostnih trikotnikov sicer operirali z efektivnimi vrednostmi napetosti. Vemo pa, da napetostni trikotnik velja tudi za '''maksimalne''' vrednosti sinusne napetosti. | Zaradi enostavnosti bomo pri obravnavi napetostnih trikotnikov sicer operirali z efektivnimi vrednostmi napetosti. Vemo pa, da napetostni trikotnik velja tudi za '''maksimalne''' vrednosti sinusne napetosti. | ||
| + | |||
Računanje količin v zaporednem krogu z uporom, tuljavo in kondenzatorjem temelji torej na enakih pravilih kot v zaporednem krogu z upornostjo in tuljavo ali kondenzatorjem. Dodatno dejstvo je v '''nasprotni kateti''' trikotnika, ki je v tem primeru '''razlika''' dveh jalovih '''napetosti''' ali '''upornosti'''. Tudi v tem primeru lahko po '''Pitagorovem''' izreku zapišemo npr.: | Računanje količin v zaporednem krogu z uporom, tuljavo in kondenzatorjem temelji torej na enakih pravilih kot v zaporednem krogu z upornostjo in tuljavo ali kondenzatorjem. Dodatno dejstvo je v '''nasprotni kateti''' trikotnika, ki je v tem primeru '''razlika''' dveh jalovih '''napetosti''' ali '''upornosti'''. Tudi v tem primeru lahko po '''Pitagorovem''' izreku zapišemo npr.: | ||
| Vrstica 24: | Vrstica 30: | ||
<latex>U\, = \,\sqrt {{U_R}^2 \,+ \,{{\left( {{U_L}\, -\, {U_C}} \right)}^2}}\,;\,\,\,\,Z \,=\, \sqrt {{R^2} \,+\, {{\left( {{X_L}\, -\, {X_C}} \right)}^2}} \,</latex> | <latex>U\, = \,\sqrt {{U_R}^2 \,+ \,{{\left( {{U_L}\, -\, {U_C}} \right)}^2}}\,;\,\,\,\,Z \,=\, \sqrt {{R^2} \,+\, {{\left( {{X_L}\, -\, {X_C}} \right)}^2}} \,</latex> | ||
| + | |||
in '''kotne''' funkcije, npr.: | in '''kotne''' funkcije, npr.: | ||
| + | |||
<latex>\csc \varphi \, =\, \frac{{{U_R}}}{U}\,;\,\,\,\,\tan \varphi \, = \,\frac{{{X_L}\, -\, {X_C}}}{R}\,\,...</latex> | <latex>\csc \varphi \, =\, \frac{{{U_R}}}{U}\,;\,\,\,\,\tan \varphi \, = \,\frac{{{X_L}\, -\, {X_C}}}{R}\,\,...</latex> | ||
| Vrstica 47: | Vrstica 55: | ||
še druge zanimive lastnosti, ki pa jih bomo obravnavali v okviru poglavja o resonančnih<ref>OE2, str. xx</ref> pojavih. | še druge zanimive lastnosti, ki pa jih bomo obravnavali v okviru poglavja o resonančnih<ref>OE2, str. xx</ref> pojavih. | ||
| - | |||
| - | |||
<primer> | <primer> | ||
Trenutna redakcija s časom 15:47, 4. september 2010
![](javascript: loadPicture("Eele_slika_3_2_9.svg", 827);)
![](javascript: loadPicture("Eele_foto_181.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_182.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_183.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_184.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_185.jpg", 1200);)
Iz sl. 3.2.8 so razvidni trije možni splošni primeri značaja izmeničnega kroga z zaporedno vezavo upora, tuljave in kondenzatorja. Iz praktičnih razlogov se za nadaljnjo obravnavo odločimo za vezavo z induktivnim značajem (sl. 3.2.9).
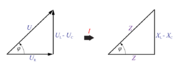
Iz kazalčnega diagrama lahko izrišemo pravokotni trikotnik napetosti s stranicami U, UR in UL – UC (sl. 3.2.9 a). Če stranice napetostnega trikotnika delimo še s skupno količino zaporednega kroga s tokom I
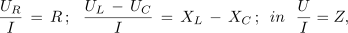
dobimo trikotnik upornosti (sl. 3.2.9 b).
- Napetosti in upornosti zaporednega kroga z uporom, tuljavo in kondenzatorjem tvorijo pravokotna trikotnika. Seštevamo jih geometrično.
Zaradi enostavnosti bomo pri obravnavi napetostnih trikotnikov sicer operirali z efektivnimi vrednostmi napetosti. Vemo pa, da napetostni trikotnik velja tudi za maksimalne vrednosti sinusne napetosti.
Računanje količin v zaporednem krogu z uporom, tuljavo in kondenzatorjem temelji torej na enakih pravilih kot v zaporednem krogu z upornostjo in tuljavo ali kondenzatorjem. Dodatno dejstvo je v nasprotni kateti trikotnika, ki je v tem primeru razlika dveh jalovih napetosti ali upornosti. Tudi v tem primeru lahko po Pitagorovem izreku zapišemo npr.:
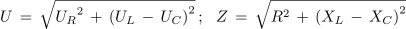
in kotne funkcije, npr.:
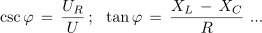
Navedene in druge enačbe reševanja pravokotnega trikotnika omogočajo pri dveh znanih količinah trikotnika računanje tretje količine.
Preskusimo prvo od dobljenih enačb na rezultatih meritev poskusa 3.2.2:
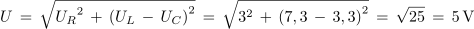
V primeru enakosti induktivne in kapacitivne upornosti ima obravnavani krog poleg lastnosti
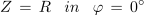
še druge zanimive lastnosti, ki pa jih bomo obravnavali v okviru poglavja o resonančnih[1] pojavih.
Primer:
1. Zaporedna vezava upora z upornostjo 30 Ω, tuljave z induktivnostjo 2 H in kondenzatorja s kapacitivnostjo 6 μF je priključena na izmenično napetost 230 V/50 Hz. Izračunaj tok in padce napetosti v električnem krogu. Kolikšen bi bil tok, če bi frekvenco spremenili tako, da bi se kapacitivna in induktivna upornost izenačili?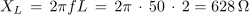
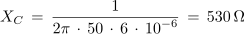
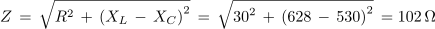
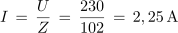
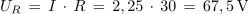
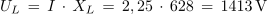
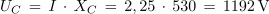
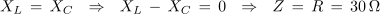
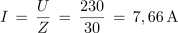
Primer:
2. Kolikšna mora biti kapacitivnost kondenzatorja, ki ga vežemo zaporedno z uporom z upornostjo 82 Ω in tuljavo z induktivnostjo 0,1 H, če želimo, da bo pri krožni frekvenci 10 4 s-1 vezava elementov povzročala fazni kot 25 º?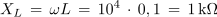
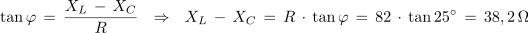
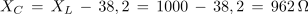
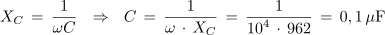
Opombe
- ↑ OE2, str. xx
 3.2.2.1 Kazalčni diagram napetosti in toka
| 3.2.2.3 Zaporedna RLC vezava (interaktivna simulacija)
|
