Iz e-ELEKTROTEHNIKA plus
| (16 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| + | <video>Eele_video_014_Vpliv_oblike_izmenicne_napetosti_na_njeno_na_njeno_efektivno_vrednost.f4v</video> | ||
| + | |||
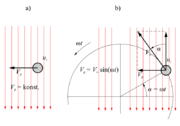
| + | [[Image:eele_slika_1_12.svg|thumb|right|Slika 1.12: Elektromagnetna indukcija napetosti]] | ||
| + | [[Image:eele_slika_1_15.svg|thumb|right|Slika 1.15: Bistvo efektivnega toka]] | ||
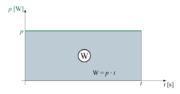
| + | [[Image:eele_slika_1_16.svg|thumb|right|Slika 1.16: Moč in delo enosmernega toka]] | ||
| + | [[Image:eele_slika_1_17.svg|thumb|right|Slika 1.17: Določanje efektivne napetosti]] | ||
| + | [[Image:eele_slika_1_18.svg|thumb|right|Slika 1.18: Časovni potek moči sinusnega toka]] | ||
| + | [[Image:eele_slika_1_19.svg|thumb|right|Slika 1.19: Moč in delo sinusnega toka]] | ||
| + | [[Image:eele_slika_1_21.svg|thumb|right|Slika 1.21: Efektivna moč sinusnega toka]] | ||
| + | [[Image:eele_slika_1_22.svg|thumb|right|Slika 1.22: Efektivna vrednost sinusne količine]] | ||
| + | [[Image:eele_foto_002.jpg|thumb|right|Fotografija 2]] | ||
| + | |||
Delo enosmernega toka računamo po enačbi<ref>Učbenik Osnove elektrotehnike 1, str. 76, enačba 423</ref>: | Delo enosmernega toka računamo po enačbi<ref>Učbenik Osnove elektrotehnike 1, str. 76, enačba 423</ref>: | ||
| + | |||
<latex>W = U \cdot I \cdot\, t = P \cdot t</latex> | <latex>W = U \cdot I \cdot\, t = P \cdot t</latex> | ||
| - | |||
| - | Za računanje dela '''izmeničnega''' toka se je pokazalo kot praktično, če ga računamo z ekvivalentnim<ref>aequivalentia, lat., iz aequus = enak in valere = veljati, pomeni '''enakovrednost'''</ref> '''enosmernim''' tokom, ki ima pri istem porabniku | + | pri čemer sta '''''U''''' in '''''I''''' vrednosti enosmernih količin. Katero vrednost pa moramo upoštevati pri računanju dela '''izmeničnega''' toka? Maksimalno, srednjo ali katero drugo vrednost? |
| + | |||
| + | |||
| + | Za računanje dela '''izmeničnega''' toka se je pokazalo kot praktično, če ga računamo z ekvivalentnim<ref>aequivalentia, lat., iz aequus = enak in valere = veljati, pomeni '''enakovrednost'''</ref> '''enosmernim''' tokom, ki ima pri istem porabniku in pri enakih pogojih '''enak učinek''' (efekt<ref>effectus, lat. = '''učinek''', posledica</ref>) kot izmenični tok. Pri segrevanju npr. vode (sl. 1.15) bi bil izmeničnemu toku ekvivalentni tok tisti enosmerni tok, ki bi isto vodo segrel z istim grelnikom v enakem času za enako temperaturno razliko. | ||
<pomembno> | <pomembno> | ||
| - | *Izmeničnemu toku po učinku ekvivalenten enosmerni tok | + | *Izmeničnemu toku po učinku ekvivalenten enosmerni tok imenujemo '''efektivni tok''' izmeničnega toka. |
| - | *Izmenični napetosti po učinku ekvivalentno enosmerno napetost | + | *Izmenični napetosti po učinku ekvivalentno enosmerno napetost imenujemo '''efektivna napetost''' izmenične napetosti. |
</pomembno> | </pomembno> | ||
| Vrstica 33: | Vrstica 48: | ||
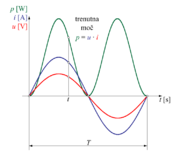
Podobno lahko sklepamo za sinusni tok. Če za posamezne trenutne vrednosti sinusnega toka in napetosti v času periode določimo trenutne moči: | Podobno lahko sklepamo za sinusni tok. Če za posamezne trenutne vrednosti sinusnega toka in napetosti v času periode določimo trenutne moči: | ||
| - | |||
| - | + | <latex>i^2 \, \cdot\, R \,= \,p{\mathrm{\,\,\,\,\,in\,\,\,\,\,(}} - i)^2 \,\cdot\,R\,= \,p,</latex> | |
| - | |||
| - | + | dobimo časovni diagram moči sinusnega toka za periodo <latex>T</latex> (slika 1.18), ki ima tudi '''sinusno''' obliko, '''dvojno frekvenco''' toka in je v času cele periode '''pozitiven'''. | |
| + | |||
| + | |||
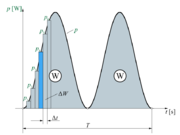
| + | Nekoliko poenostavljeno bi v tem primeru lahko »izračunali« delo tako, da bi sešteli delčke dela <latex>\Delta W</latex>, izračunane na osnovi povprečnih trenutnih moči v čim krajših časovnih intervalih <latex>\Delta T</latex> (slika 1.19). | ||
| + | |||
| + | |||
| + | Ker je posamezni delček dela <latex>\Delta W</latex> ponazorjen z delčkom površine, ki jo v času <latex>\Delta T</latex> oklene diagram moči s časovno osjo, lahko za celotno delo sklepamo: | ||
| Vrstica 48: | Vrstica 67: | ||
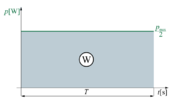
Računanje električnega dela na omenjeni način ni praktično. Ker pri računanju dela v bistvu računamo »površino« (slika 1.19), si lahko pomagamo tako, kot to prikazujeta sliki 1.20 in 1.21. Na osnovi slike 1.20 lahko zapišemo: | Računanje električnega dela na omenjeni način ni praktično. Ker pri računanju dela v bistvu računamo »površino« (slika 1.19), si lahko pomagamo tako, kot to prikazujeta sliki 1.20 in 1.21. Na osnovi slike 1.20 lahko zapišemo: | ||
| + | |||
<latex>W\, = \,\frac{P_{\mathrm {m}}} {2}\, \cdot\, T</latex> ali za poljuben čas t: <latex>W \,=\, \frac{P_{\mathrm {m}}}{2} \,\cdot\, t</latex> | <latex>W\, = \,\frac{P_{\mathrm {m}}} {2}\, \cdot\, T</latex> ali za poljuben čas t: <latex>W \,=\, \frac{P_{\mathrm {m}}}{2} \,\cdot\, t</latex> | ||
| + | |||
Predpostavimo, da sta '''enosmerni''' in '''izmenični''' tok pri '''enakem porabniku''' v '''enakem času''' opravila '''enako delo'''. V tem primeru sta površini pod pripadajočima diagramoma moči (sl. 1.16 in sl. 1.21) enaki. Iz enačbe | Predpostavimo, da sta '''enosmerni''' in '''izmenični''' tok pri '''enakem porabniku''' v '''enakem času''' opravila '''enako delo'''. V tem primeru sta površini pod pripadajočima diagramoma moči (sl. 1.16 in sl. 1.21) enaki. Iz enačbe | ||
| + | |||
<latex>P = \frac{P_{\rm {m}}}{2}||| (W)|||'''Enačba 1.10'''</latex> | <latex>P = \frac{P_{\rm {m}}}{2}||| (W)|||'''Enačba 1.10'''</latex> | ||
| Vrstica 64: | Vrstica 86: | ||
Če upoštevamo, da je <latex>P \, = \,I^2 \, \cdot\, R\,</latex> in <latex> P_{\mathrm{m}}\, = \,I_{\mathrm{m}}^2\,\cdot\, R</latex> dobimo: | Če upoštevamo, da je <latex>P \, = \,I^2 \, \cdot\, R\,</latex> in <latex> P_{\mathrm{m}}\, = \,I_{\mathrm{m}}^2\,\cdot\, R</latex> dobimo: | ||
| - | |||
| - | <latex>I\, =\, \frac{I_{\mathrm{m}} }{ | + | <latex>I^2 \, \cdot\, R\, = \,\frac{I_{\mathrm{m}}^2\,\cdot\, R}{2}</latex> ali <latex> I^2\, = \,\frac{I_{\mathrm{m}}^2 }{2}</latex> |
| - | <latex>I \,= \,70,7{\rm{\, \% \, }}\cdot\,I_{\rm{m}}|||(A)|||'''Enačba 1.11'''</latex> | + | |
| + | in od tod: | ||
| + | |||
| + | |||
| + | <latex>I\, =\, \frac{I_{\mathrm{m}} }{\sqrt 2 } \,= \,70,7{\rm{\, \% \, }}\cdot\,I_{\rm{m}}|||(A)|||'''Enačba 1.11'''</latex>. | ||
<pomembno> | <pomembno> | ||
| - | *Efektivni tok je | + | *Efektivni tok je <latex>\sqrt 2</latex>-krat manjši od maksimalne vrednosti sinusnega toka (sl. 1.22). |
</pomembno> | </pomembno> | ||
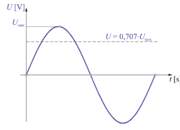
| - | Na osnovi enačbe | + | Na osnovi enačbe <latex>P=U^2/R</latex> dobimo še '''efektivno''' vrednost sinusne napetosti<ref>Zaradi '''kvadratne''' odvisnosti moči sinusnega toka <latex>P=I^2\cdot R</latex> ali tudi <latex>P=U^2/R</latex> pravimo efektivni vrednosti sinusne količine tudi '''srednja kvadratna''' ali '''geometrična srednja vrednost''' sinusne količine.</ref>. |
| + | |||
| - | <latex>U\, =\, \frac{U_{\mathrm{m}} }{\sqrt 2 }|||(V) | + | <latex>U\, =\, \frac{U_{\mathrm{m}} }{\sqrt 2 } \,= \,70,7{\rm{\, \% \, }}\cdot\,U_{\rm{m}}|||(V)|||'''Enačba 1.12'''</latex>. |
| - | |||
| - | Ocena rezultatov poskusa 1.1.2 je | + | Ocena rezultatov poskusa 1.1.2 je bila torej pravilna. Enako velja za vse električne količine, katerih izvor sta sinusna napetost in tok, kot sta npr. električna in magnetna poljska jakost ... |
| Vrstica 91: | Vrstica 116: | ||
| - | Maksimalne vrednosti izmeničnih električnih količin v praksi praviloma niso znane | + | Maksimalne vrednosti izmeničnih električnih količin v praksi praviloma niso znane, zato je za računanje učinkov na osnovi merjenja teh količin, poskrbljeno z izvedbo merilnikov. |
| Vrstica 99: | Vrstica 124: | ||
| - | Poudarjanje »efektivna vrednost«, praviloma | + | Poudarjanje »efektivna vrednost«, praviloma iz praktičnih razlogov, opustimo. Če torej rečemo, zapišemo ali preberemo »izmenična napetost 230 V«, gre za '''efektivno''' vrednost izmenične napetosti, njena maksimalna vrednost pa je <latex>\sqrt{2}</latex>-krat večja. |
| - | |||
<primer> | <primer> | ||
| - | |||
Pri merjenju izmenične napetosti električnega omrežja pokaže V-meter 230 V. Kolikšni sta efektivna in maksimalna vrednost napetosti v omrežju? Prikaži obe vrednosti grafično.||| | Pri merjenju izmenične napetosti električnega omrežja pokaže V-meter 230 V. Kolikšni sta efektivna in maksimalna vrednost napetosti v omrežju? Prikaži obe vrednosti grafično.||| | ||
| Vrstica 112: | Vrstica 135: | ||
</primer> | </primer> | ||
<primer> | <primer> | ||
| - | |||
Električni grelnik z upornostjo 10 Ω priključimo na sinusno napetost 230 V. Kolikšen tok skozi porabnik pokaže A-meter, kolikšna je maksimalna vrednost toka in kolikšno električno delo opravi tok v času 8 ur?||| | Električni grelnik z upornostjo 10 Ω priključimo na sinusno napetost 230 V. Kolikšen tok skozi porabnik pokaže A-meter, kolikšna je maksimalna vrednost toka in kolikšno električno delo opravi tok v času 8 ur?||| | ||
| Vrstica 134: | Vrstica 156: | ||
| + | <references/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 08:08, 27. oktober 2010
Delo enosmernega toka računamo po enačbi[1]:
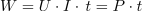
pri čemer sta U in I vrednosti enosmernih količin. Katero vrednost pa moramo upoštevati pri računanju dela izmeničnega toka? Maksimalno, srednjo ali katero drugo vrednost?
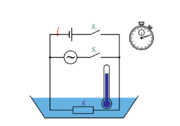
Za računanje dela izmeničnega toka se je pokazalo kot praktično, če ga računamo z ekvivalentnim[2] enosmernim tokom, ki ima pri istem porabniku in pri enakih pogojih enak učinek (efekt[3]) kot izmenični tok. Pri segrevanju npr. vode (sl. 1.15) bi bil izmeničnemu toku ekvivalentni tok tisti enosmerni tok, ki bi isto vodo segrel z istim grelnikom v enakem času za enako temperaturno razliko.
- Izmeničnemu toku po učinku ekvivalenten enosmerni tok imenujemo efektivni tok izmeničnega toka.
- Izmenični napetosti po učinku ekvivalentno enosmerno napetost imenujemo efektivna napetost izmenične napetosti.
Poskus 1.2:
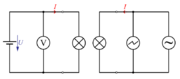
Eno od dveh enakih žarnic, npr. 12 V/100 mA, priključimo na enosmerno, drugo pa na sinusno izmenično napetost (sl. 1.17) tako, da žarilni nitki žarita enako. Enosmerno napetost primerjajmo z maksimalno vrednostjo izmenične napetosti, ki jo dobimo z opazovanjem izmenične napetosti na osciloskopu.
- Enosmerna napetost, ki požene tok z enakim učinkom kot sinusna napetost, je približno 70 % maksimalne vrednosti sinusne napetosti.
Bolj točen odgovor na to vprašanje poiščimo z znanjem o enosmernem električnem toku in s sklepanjem (slika 1.16).
- Delo enosmernega električnega toka je določeno s »površino«, ki jo oklepa krivulja moči s časovno osjo.
Podobno lahko sklepamo za sinusni tok. Če za posamezne trenutne vrednosti sinusnega toka in napetosti v času periode določimo trenutne moči:
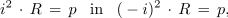
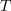
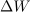
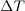
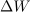
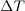
- Delo izmeničnega toka je določeno s »površino«, ki jo oklepata krivulja moči izmeničnega toka in časovna os.
Računanje električnega dela na omenjeni način ni praktično. Ker pri računanju dela v bistvu računamo »površino« (slika 1.19), si lahko pomagamo tako, kot to prikazujeta sliki 1.20 in 1.21. Na osnovi slike 1.20 lahko zapišemo:
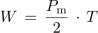
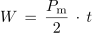
Predpostavimo, da sta enosmerni in izmenični tok pri enakem porabniku v enakem času opravila enako delo. V tem primeru sta površini pod pripadajočima diagramoma moči (sl. 1.16 in sl. 1.21) enaki. Iz enačbe
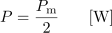
- Moč efektivnega toka je efektivna moč izmeničnega toka.
- Efektivna moč sinusnega toka (P) je enaka polovici njegove maksimalne moči.
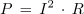
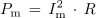
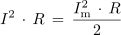
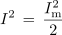
in od tod:
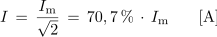
- Efektivni tok je -krat manjši od maksimalne vrednosti sinusnega toka (sl. 1.22).
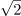
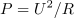
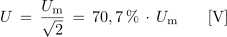
Ocena rezultatov poskusa 1.1.2 je bila torej pravilna. Enako velja za vse električne količine, katerih izvor sta sinusna napetost in tok, kot sta npr. električna in magnetna poljska jakost ...
- Efektivne vrednosti izmeničnih količin označujemo enako kot enosmerne količine.
- Učinke izmeničnih električnih količin računamo z njihovimi efektivnimi vrednostmi na osnovi zakonitosti za enosmerne količine.
Maksimalne vrednosti izmeničnih električnih količin v praksi praviloma niso znane, zato je za računanje učinkov na osnovi merjenja teh količin, poskrbljeno z izvedbo merilnikov.
- Merilniki izmeničnih količin kažejo efektivne vrednosti.
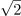
Primer:
Pri merjenju izmenične napetosti električnega omrežja pokaže V-meter 230 V. Kolikšni sta efektivna in maksimalna vrednost napetosti v omrežju? Prikaži obe vrednosti grafično.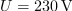
Maksimalna napetost:
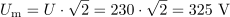
Primer:
Električni grelnik z upornostjo 10 Ω priključimo na sinusno napetost 230 V. Kolikšen tok skozi porabnik pokaže A-meter, kolikšna je maksimalna vrednost toka in kolikšno električno delo opravi tok v času 8 ur?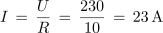
Maksimalni tok:
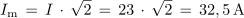
Električno delo:
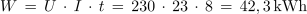
Če bi na podoben način kot za sinusno obliko razmislili tudi za druge oblike izmeničnih količin, bi ugotovili:
- Efektivna vrednost izmenične količine je odvisna tudi od oblike njenega časovnega poteka.
Za primerjavo z efektivno vrednostjo sinusne oblike izmenične količine se informativno seznanimo z efektivnimi vrednostmi nekaterih pogostejših oblik časovnih potekov izmeničnih količin (pregl. 1.12):
Opombe
- ↑ Učbenik Osnove elektrotehnike 1, str. 76, enačba 423
- ↑ aequivalentia, lat., iz aequus = enak in valere = veljati, pomeni enakovrednost
- ↑ effectus, lat. = učinek, posledica
- ↑ Zaradi kvadratne odvisnosti moči sinusnega toka ali tudi
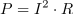 pravimo efektivni vrednosti sinusne količine tudi srednja kvadratna ali geometrična srednja vrednost sinusne količine.
pravimo efektivni vrednosti sinusne količine tudi srednja kvadratna ali geometrična srednja vrednost sinusne količine.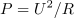
| | 1.4 Srednja vrednost periodične količine |