Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (3 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | Polnilni tok kondenzatorja je sorazmeren hitrosti spreminjanja njegove napetosti. Takrat smo to zapisali s kvocientom prirastkov napetosti in časa, v mislih pa imeli kar najkrajši | + | Polnilni tok kondenzatorja je sorazmeren hitrosti spreminjanja njegove napetosti. Takrat smo to zapisali s kvocientom prirastkov napetosti in časa, v mislih pa imeli kar najkrajši <latex>\Delta t</latex>. Po novem bomo to pisali z odvodom, |
| + | |||
<latex>{i\, = \,C\frac{\Delta u}{\Delta t}{\rm{ (}}\Delta t{\rm{\,\, cim\,\, krajsi) }} \,\,\,\,\Rightarrow \,\,\,\,{\rm{ }}i\, =\, C\frac{{\rm{d}}u}{{\rm{d}}t} \,=\, Cu^\prime {\rm{ }} \,\,\,\,\Rightarrow \,\,\,\,{\rm{ d}}u \,=\, u^\prime {\rm{d}}t\, = \,\frac{i}{C}{\rm{d}}t,}</latex> | <latex>{i\, = \,C\frac{\Delta u}{\Delta t}{\rm{ (}}\Delta t{\rm{\,\, cim\,\, krajsi) }} \,\,\,\,\Rightarrow \,\,\,\,{\rm{ }}i\, =\, C\frac{{\rm{d}}u}{{\rm{d}}t} \,=\, Cu^\prime {\rm{ }} \,\,\,\,\Rightarrow \,\,\,\,{\rm{ d}}u \,=\, u^\prime {\rm{d}}t\, = \,\frac{i}{C}{\rm{d}}t,}</latex> | ||
| - | brali pa: polnilni tok kondenzatorja je enak produktu kapacitivnosti in odvoda napetosti | + | |
| + | brali pa: polnilni tok kondenzatorja je enak produktu kapacitivnosti in odvoda napetosti. Zaradi tega je diferencial napetosti enak produktu odvoda napetosti in diferenciala časa. Podobno bo s tokom in napetostjo pri tuljavi: | ||
| + | |||
<latex>{u\, =\, L\frac{\Delta i}{\Delta t}{\rm{ (}}\Delta t{\rm{\,\, cim\,\, krajsi) }} \,\,\,\,\Rightarrow\,\,\,\, {\rm{ }}u \,=\, L\frac{{\rm{d}}i}{{\rm{d}}t}\, =\, Li^\prime {\rm{ }}\,\,\,\, \Rightarrow \,\,\,\,{\rm{ d}}i\, =\, i^\prime {\rm{d}}t\, =\, \frac{u}{L}{\rm{d}}t.}</latex> | <latex>{u\, =\, L\frac{\Delta i}{\Delta t}{\rm{ (}}\Delta t{\rm{\,\, cim\,\, krajsi) }} \,\,\,\,\Rightarrow\,\,\,\, {\rm{ }}u \,=\, L\frac{{\rm{d}}i}{{\rm{d}}t}\, =\, Li^\prime {\rm{ }}\,\,\,\, \Rightarrow \,\,\,\,{\rm{ d}}i\, =\, i^\prime {\rm{d}}t\, =\, \frac{u}{L}{\rm{d}}t.}</latex> | ||
| - | |||
| - | Moč pritekanja energije v električni element je enaka hitrosti spreminjanja energije (električne, magnetne | + | Napetost tuljave je enaka produktu induktivnosti in odvoda toka, diferencial toka je enak produktu odvoda toka in diferenciala časa. |
| + | |||
| + | |||
| + | Moč pritekanja energije v električni element je enaka hitrosti spreminjanja energije (električne, magnetne ali toplote): | ||
| + | |||
<latex>{p\, = \,\frac{\Delta W}{\Delta t}{\rm{ (}}\Delta t{\rm{\,\, cim\,\, krajsi) }}\,\,\,\, \Rightarrow\,\,\,\, {\rm{ }}p \,=\, \frac{{\rm{d}}W}{{\rm{d}}t}\, =\, W^\prime {\rm{ }} \,\,\,\,\Rightarrow\,\,\,\, {\rm{ d}}W\, =\, W^\prime {\rm{d}}t \,=\, p{\rm{d}}t.}</latex> | <latex>{p\, = \,\frac{\Delta W}{\Delta t}{\rm{ (}}\Delta t{\rm{\,\, cim\,\, krajsi) }}\,\,\,\, \Rightarrow\,\,\,\, {\rm{ }}p \,=\, \frac{{\rm{d}}W}{{\rm{d}}t}\, =\, W^\prime {\rm{ }} \,\,\,\,\Rightarrow\,\,\,\, {\rm{ d}}W\, =\, W^\prime {\rm{d}}t \,=\, p{\rm{d}}t.}</latex> | ||
| + | |||
Odvajajmo funkciji energij v kondenzatorju in tuljavi: | Odvajajmo funkciji energij v kondenzatorju in tuljavi: | ||
| + | |||
<latex>\frac{{\rm{d}}{W_{\rm{e}}}}{{\rm{d}}t}\, =\, ({\textstyle{1 \over 2}}C{u^2})^\prime \, =\, {\textstyle{1 \over 2}}C({u^2})^\prime \, = \,{\textstyle{1 \over 2}}C(2u)u^\prime \, =\, Cu^\prime u\, =\, ui.</latex> | <latex>\frac{{\rm{d}}{W_{\rm{e}}}}{{\rm{d}}t}\, =\, ({\textstyle{1 \over 2}}C{u^2})^\prime \, =\, {\textstyle{1 \over 2}}C({u^2})^\prime \, = \,{\textstyle{1 \over 2}}C(2u)u^\prime \, =\, Cu^\prime u\, =\, ui.</latex> | ||
| + | |||
<latex>\frac{{\rm{d}}{W_{\rm{m}}}}{{\rm{d}}t} \,=\, ({\textstyle{1 \over 2}}L{i^2})^\prime \, =\, {\textstyle{1 \over 2}}L({i^2})^\prime \, =\, {\textstyle{1 \over 2}}L(2i)i^\prime \, =\, Li^\prime i \,=\, ui.</latex> | <latex>\frac{{\rm{d}}{W_{\rm{m}}}}{{\rm{d}}t} \,=\, ({\textstyle{1 \over 2}}L{i^2})^\prime \, =\, {\textstyle{1 \over 2}}L({i^2})^\prime \, =\, {\textstyle{1 \over 2}}L(2i)i^\prime \, =\, Li^\prime i \,=\, ui.</latex> | ||
| - | Upoštevali smo lastnosti odvajanja in dobili: moč polnjenja enega ali drugega elementa je vsakokrat enaka produktu toka in napetosti. Določene prednosti odvoda že vidimo | + | |
| + | Upoštevali smo lastnosti odvajanja in dobili: moč polnjenja enega ali drugega elementa je vsakokrat enaka produktu toka in napetosti. Določene prednosti odvoda že vidimo, zapisi so preglednejši in nič ni več potrebno pripominjati, da je prirastek <latex>\Delta t</latex> čim krajši, saj je kot tak zajet že v sami definiciji odvoda. | ||
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 19:08, 12. julij 2010
Polnilni tok kondenzatorja je sorazmeren hitrosti spreminjanja njegove napetosti. Takrat smo to zapisali s kvocientom prirastkov napetosti in časa, v mislih pa imeli kar najkrajši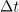
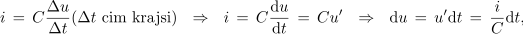
brali pa: polnilni tok kondenzatorja je enak produktu kapacitivnosti in odvoda napetosti. Zaradi tega je diferencial napetosti enak produktu odvoda napetosti in diferenciala časa. Podobno bo s tokom in napetostjo pri tuljavi:
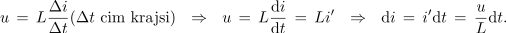
Napetost tuljave je enaka produktu induktivnosti in odvoda toka, diferencial toka je enak produktu odvoda toka in diferenciala časa.
Moč pritekanja energije v električni element je enaka hitrosti spreminjanja energije (električne, magnetne ali toplote):
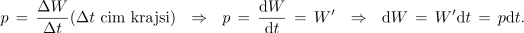
Odvajajmo funkciji energij v kondenzatorju in tuljavi:
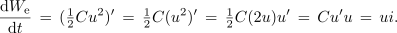
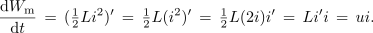
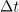
| | 5.4 Določen integral funkcije |
