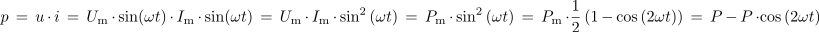Iz e-ELEKTROTEHNIKA plus
| Vrstica 38: | Vrstica 38: | ||
| - | Prepričali se bomo, da plastne upore kot sta upora v poskusu 3.1.2, lahko pri nizki frekvenci obravnavamo kot upora s praktično čisto ohmsko upornostjo (idealna upora). Zato lahko sklepamo: | + | Prepričali se bomo, da plastne upore, kot sta upora v poskusu 3.1.2, lahko pri nizki frekvenci obravnavamo kot upora s praktično čisto ohmsko upornostjo (idealna upora). Zato lahko sklepamo: |
<pomembno> | <pomembno> | ||
| Vrstica 57: | Vrstica 57: | ||
| - | vstavimo izraz za trenutno vrednost sinusne napetost ''u'' = ''U''<sub>m</sub> ∙ sin(''ωt''): | + | vstavimo izraz za trenutno vrednost sinusne napetost ''u'' = ''U''<sub>m</sub> ∙ sin (''ωt''): |
<latex>i\,=\, \frac {U_{\rm{m}}\, \cdot\,{\rm{sin}}\,(\omega t) }{R}\, = \,\frac {U_{\rm{m}}}{R}\, \cdot\,{\rm{sin}}\,(\omega t) </latex> | <latex>i\,=\, \frac {U_{\rm{m}}\, \cdot\,{\rm{sin}}\,(\omega t) }{R}\, = \,\frac {U_{\rm{m}}}{R}\, \cdot\,{\rm{sin}}\,(\omega t) </latex> | ||
| Vrstica 83: | Vrstica 83: | ||
| - | Delovna upornost je v širšem smislu vsaka upornost, '''dejanska''' ali le '''navidezna''', ki povzroča ali omogoča '''trajno pretvorbo''' električne energije v energije '''drugih oblik'''. Dejanske ohmske upornosti (grelniki, žarnice, upori, vodniki …) | + | Delovna upornost je v širšem smislu vsaka upornost, '''dejanska''' ali le '''navidezna''', ki povzroča ali omogoča '''trajno pretvorbo''' električne energije v energije '''drugih oblik'''. Dejanske ohmske upornosti (grelniki, žarnice, upori, vodniki …) lahko neposredno izmerimo z Ω-metrom, navidezne pa praviloma določimo posredno, računsko, na osnovi merjenja drugih količin in le pri '''delovanju''' naprav. Tak primer imamo kot del energije pri pretvorbi električne energije v '''mehansko''' (elektromotor), v '''zvočno''' (zvočniki), v energijo '''elektromagnetnega valovanja''' (oddajniki) in podobno. |
<pomembno> | <pomembno> | ||
| Vrstica 91: | Vrstica 91: | ||
| - | O moči sinusnega izmeničnega toka smo sicer nekaj že izvedeli<ref>OE2, str. 7-8</ref>, zato bomo za izmenični krog s čisto delovno upornostjo | + | O moči sinusnega izmeničnega toka smo sicer nekaj že izvedeli<ref>OE2, str. 7-8</ref>, zato bomo za izmenični krog s čisto delovno upornostjo že znano le dopolnili. Z upoštevanjem časovnih potekov napetosti in toka v ohmskem izmeničnem krogu (slika 3.1.4) in dejstva, da je trenutna moč določena s produktom trenutne napetosti in trenutnega toka |
| - | <latex>p\,=\, u\, \cdot \,i</latex> | + | <latex>p\,=\, u\, \cdot \,i,</latex> |
dobimo še časovni potek moči v ohmskem izmeničnem krogu (slika 3.1.5) | dobimo še časovni potek moči v ohmskem izmeničnem krogu (slika 3.1.5) | ||
<pomembno> | <pomembno> | ||
| - | *Časovni potek moči sinusnega izmeničnega toka ima pri ohmski upornosti '''sinusno obliko''' z '''dvojno frekvenco'''<ref><latex>p \, = \,u\,\cdot\,i\,=\,U_{\rm{m}}\,\cdot\,{\rm{sin}}(\omega t)\,\cdot\,I_{\rm{m}}\,\cdot\,{\rm{sin}}(\omega t)\,=\,U_{\rm{m}}\,\cdot\,I_{\rm{m}}\,\cdot\,{\rm{sin}}^2 \,(\omega t)\,=\,P_{\rm{m}}\,\cdot\,{\rm{sin}}^2 \,(\omega t)\,=\,P_{\rm{m}}\,\cdot\frac{1}{2}\, (1\,-\,{\rm{cos}}\,(2 \omega t) ) \,=\,P\,-\,P\,\cdot {\rm{cos}}\,(2 \omega t)</latex></ref> toka oziroma napetosti.</pomembno> | + | *Časovni potek moči sinusnega izmeničnega toka ima pri ohmski upornosti '''sinusno obliko''' z '''dvojno frekvenco'''<ref><latex>p \, = \,u\,\cdot\,i\,=\,U_{\rm{m}}\,\cdot\,{\rm{sin }}(\omega t)\,\cdot\,I_{\rm{m}}\,\cdot\,{\rm{sin }}(\omega t)\,=\,U_{\rm{m}}\,\cdot\,I_{\rm{m}}\,\cdot\,{\rm{sin}}^2 \,(\omega t)\,=\,P_{\rm{m}}\,\cdot\,{\rm{sin}}^2 \,(\omega t)\,=\,P_{\rm{m}}\,\cdot\frac{1}{2}\, (1\,-\,{\rm{cos}}\,(2 \omega t) ) \,=\,P\,-\,P\,\cdot {\rm{cos}}\,(2 \omega t)</latex></ref> toka oziroma napetosti.</pomembno> |
Površina pod krivuljo moči delovnega toka je v celoti pozitivna, kar pomeni, da energija teče samo '''iz generatorja v porabnik''', kjer se '''trajno''' pretvarja v energije drugih oblik in '''sprošča''' iz električnega kroga. | Površina pod krivuljo moči delovnega toka je v celoti pozitivna, kar pomeni, da energija teče samo '''iz generatorja v porabnik''', kjer se '''trajno''' pretvarja v energije drugih oblik in '''sprošča''' iz električnega kroga. | ||
| Vrstica 114: | Vrstica 114: | ||
<latex>P\,=\, I^2\, \cdot \,R \,=\,\frac{U^2}{R}|||(W)</latex> | <latex>P\,=\, I^2\, \cdot \,R \,=\,\frac{U^2}{R}|||(W)</latex> | ||
| - | Na osnovi odvisnosti efektivne in maksimalne vrednosti sinusne napetosti in toka ter slike 3.1.8 | + | Na osnovi odvisnosti efektivne in maksimalne vrednosti sinusne napetosti in toka ter slike 3.1.8 lahko določimo tudi '''maksimalno delovno''' moč: |
<latex>P_{\rm{m}}\,=\, U_{\rm{m}}\, \cdot \,I_{\rm{m}} \,=\,\sqrt{2}\cdot \,U\,\cdot \,\sqrt{2}\, \cdot \,I \, = \, 2UI \, = \, 2P |||(W)</latex> | <latex>P_{\rm{m}}\,=\, U_{\rm{m}}\, \cdot \,I_{\rm{m}} \,=\,\sqrt{2}\cdot \,U\,\cdot \,\sqrt{2}\, \cdot \,I \, = \, 2UI \, = \, 2P |||(W)</latex> | ||
| Vrstica 137: | Vrstica 137: | ||
*Delovna moč je odvisna tudi od '''oblike''' časovnega poteka izmenične napetosti oziroma toka. | *Delovna moč je odvisna tudi od '''oblike''' časovnega poteka izmenične napetosti oziroma toka. | ||
</primer> | </primer> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
Redakcija: 16:02, 7. maj 2010
Ohmskih porabnikov je v praksi veliko. To so na področju energetike npr. uporovni grelniki in svetila z žarilno nitko, v elektroniki pa najrazličnejši upori kot elementi elektronskih vezij.
Ohmski upor v enosmernem in izmeničnem krogu
Poskus 3.1.1:
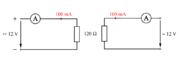
Upora z upornostjo npr. 120 Ω priključimo prek A-metrov na enosmerno in izmenično napetost 12 V/50 Hz (sl. 3.1.2). Primerjajmo efektivni tok izmeničnega kroga s tokom enosmernega kroga.
- Efektivni tok v izmeničnem krogu je enak toku v enosmernem krogu.
- Porabnik s čisto ohmsko upornostjo enako prevaja enosmerni in izmenični tok.
Časovni potek napetosti in toka
Poskus 3.1.2:
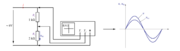
Na izvor sinusne izmenične napetosti npr. 6 V /50 Hz priključimo zaporedno vezavo plastnih uporov 1000 Ω in 2000 Ω (slika 3.1.3). Na dvokanalnem osciloskopu primerjajmo časovna poteka napetosti izvora in padca napetosti na R2 .
- Obliki časovnih potekov napetosti izvora in padca napetosti na uporu sta sinusni – enaki.
- Padec napetosti na uporu je v fazi z napetostjo izvora.
Prek padca napetosti na ohmski upornosti posredno opazujemo tudi časovni potek toka. Iz do sedaj spoznanih dejstev o električnem toku namreč vemo, da je tok skozi konstantno ohmsko upornost premo sorazmeren z napetostjo:
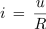
Prepričali se bomo, da plastne upore, kot sta upora v poskusu 3.1.2, lahko pri nizki frekvenci obravnavamo kot upora s praktično čisto ohmsko upornostjo (idealna upora). Zato lahko sklepamo:
- Sinusna izmenična napetost požene v električnem krogu s čisto ohmsko upornostjo sinusni izmenični tok, ki je v fazi z napetostjo.
Velja tudi obratno:
Obe ugotovitvi nazorno prikazuje slika 3.1.4.
O ugotovitvi se lahko prepričamo tudi po matematični poti. V Ohmov zakon za trenutno vrednost toka
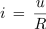
vstavimo izraz za trenutno vrednost sinusne napetost u = Um ∙ sin (ωt):
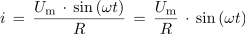

Primerjava izrazov trenutnih vrednosti sinusne napetosti in toka potrjuje identičnost in sočasnost časovnih potekov obeh količin v ohmskem izmeničnem krogu.
Energija in moč v ohmskem izmeničnem krogu (W, P)
Poskus 3.1.3:
Poskus 2.1.1 ponovimo namesto z uporoma z enakima žarnicama, npr. 12 V/0,1 A.
- Žarnici svetita enako, v obeh je enak efektivni tok.
Poskus bi lahko ponovili z električnima grelnikoma in rezultat bi bil podoben.
- Upornost, ki povzroča enak učinek enosmernega in izmeničnega toka, imenujemo delovna upornost.
Delovna upornost je v širšem smislu vsaka upornost, dejanska ali le navidezna, ki povzroča ali omogoča trajno pretvorbo električne energije v energije drugih oblik. Dejanske ohmske upornosti (grelniki, žarnice, upori, vodniki …) lahko neposredno izmerimo z Ω-metrom, navidezne pa praviloma določimo posredno, računsko, na osnovi merjenja drugih količin in le pri delovanju naprav. Tak primer imamo kot del energije pri pretvorbi električne energije v mehansko (elektromotor), v zvočno (zvočniki), v energijo elektromagnetnega valovanja (oddajniki) in podobno.
- Električna energija v delovni obliki zapusti električni krog. Imenujemo jo delovna energija.
- Električni tok v izmeničnem krogu s čisto delovno upornostjo imenujemo delovni tok.
- Delovni izmenični tok je tok, ki je v fazi z napetostjo (φ = 0°).
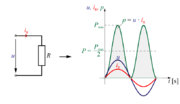
O moči sinusnega izmeničnega toka smo sicer nekaj že izvedeli[1], zato bomo za izmenični krog s čisto delovno upornostjo že znano le dopolnili. Z upoštevanjem časovnih potekov napetosti in toka v ohmskem izmeničnem krogu (slika 3.1.4) in dejstva, da je trenutna moč določena s produktom trenutne napetosti in trenutnega toka
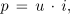
dobimo še časovni potek moči v ohmskem izmeničnem krogu (slika 3.1.5)
- Časovni potek moči sinusnega izmeničnega toka ima pri ohmski upornosti sinusno obliko z dvojno frekvenco[2] toka oziroma napetosti.
Površina pod krivuljo moči delovnega toka je v celoti pozitivna, kar pomeni, da energija teče samo iz generatorja v porabnik, kjer se trajno pretvarja v energije drugih oblik in sprošča iz električnega kroga.
- Moč delovnega toka imenujemo delovna moč (P), merimo jo v vatih (W).
- V primeru faznega kota φ = 0° je v izmeničnem krogu prisotna delovna moč.
- Efektivna delovna moč je določena s produktom efektivne napetosti in efektivnega delovnega toka.
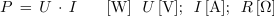
velja pa tudi
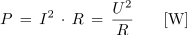
Na osnovi odvisnosti efektivne in maksimalne vrednosti sinusne napetosti in toka ter slike 3.1.8 lahko določimo tudi maksimalno delovno moč:
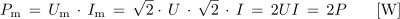
ali
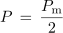
Opozoriti pa moramo, da dobljena enačba za delovno moč velja le za sinusno obliko delovnega toka.
Primer:
Primer:Upor z upornostjo 40 Ω priključimo zapovrstjo na izmenično napetost sinusne in trikotne oblike. Izračunaj efektivne delovne moči, če je maksimalna napetost v obeh primerih 10 V. Uporabi vrednosti iz preglednice 1.2.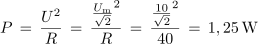
2. Trikotna oblika:
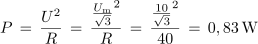
*Delovna moč je odvisna tudi od oblike časovnega poteka izmenične napetosti oziroma toka.
Opombe
Podpoglavja:
- 3.1.1.1 Ohmski upor v enosmernem in izmeničnem krogu
- 3.1.1.2 Časovni potek napetosti in toka
- 3.1.1.3 Energija in moč v ohmskem izmeničnem krogu
| | 3.1.1.1 Ohmski upor v enosmernem in izmeničnem krogu |