5.3 Odvod funkcije

Iz e-ELEKTROTEHNIKA plus

Redakcija: 19:14, 12. julij 2010 (view source) Admin (Pogovor | prispevki) ← Starejša redakcija		Redakcija: 19:15, 12. julij 2010 (view source) Admin (Pogovor | prispevki) Novejše urejanje →
Vrstica 5:		Vrstica 5:
-	Znak »<latex>\mathop {\lim }</latex>« je okrajšava za ''limito'', znak razlike »&Delta;« pa preide v ''diferencialni'' znak »d«. Novi, infinitezimalni količini d''t'' in d''f'' sta ''diferenciala'' neodvisne in odvisne spremenljivke. Ker je odvod funkcije ''f'' v splošnem tudi funkcija, se za odvod uporablja tudi nekvocientni zapis »''f''&prime;«. Diferencial d''f'' določa torej produkt odvoda ''f''&prime; in diferenciala d''t''.	+	Znak »<latex>\mathop {\lim }</latex>« je okrajšava za ''limito'', znak razlike »<latex>\Delta</latex>« pa preide v ''diferencialni'' znak »<latex>{\mathrm{d}}</latex>«. Novi, infinitezimalni količini <latex>{\mathrm{d}}t</latex> in <latex>{\mathrm{d}}f</latex> sta ''diferenciala'' neodvisne in odvisne spremenljivke. Ker je odvod funkcije <latex>f</latex> v splošnem tudi funkcija, se za odvod uporablja tudi nekvocientni zapis »''f''&prime;«. Diferencial d''f'' določa torej produkt odvoda ''f''&prime; in diferenciala d''t''.

---

Redakcija: 19:15, 12. julij 2010

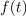
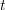
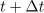
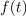
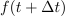
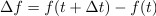
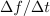
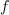
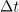
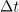
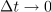
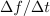
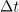
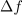
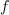
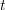
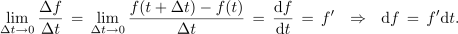
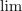
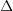
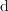
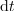
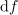
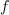
Imejmo časovno funkcijo , ki podaja napetost, morda moč, tok, naboj ali energijo (slika 1). Izberimo bližnja trenutka in . Upati smemo, da si bosta blizu tudi funkcijski vrednosti in . Prirastek je pomemben, verjetno pa tudi kvocient , ki ugotavlja hitrost spreminjanja funkcije . Informacija o njej bo najboljša takrat, ko bo interval kar najkrajši, ko bo limitiral k nič, kar povzema zapis: . Če bo tako, se bo nekaj limitnega dogajalo tudi s kvocientom . Ko se bo manjšal imenovalec , se bo z njim manjšal tudi števec , in upamo lahko, da bo k neki vrednosti limitiral tudi njun kvocient. Vrednost, h kateri stremi, imenujemo odvod funkcije ob času . Odvod pišemo takole:

Znak »« je okrajšava za limito, znak razlike »« pa preide v diferencialni znak »«. Novi, infinitezimalni količini in sta diferenciala neodvisne in odvisne spremenljivke. Ker je odvod funkcije v splošnem tudi funkcija, se za odvod uporablja tudi nekvocientni zapis »f′«. Diferencial df določa torej produkt odvoda f′ in diferenciala dt.

Najpreprostejša je konstantna funkcija: g(t) = C. Upodablja jo premica, ki je vzporedna abscisni osi. Pri vsakem intervalu Δt je Δg = 0, odvod konstante je nič. Odvod linearne funkcije h(t) = kt + n je h′ = k, saj je Δh = kΔt; o drugih več kasneje. Izpostavimo tudi nekaj lastnosti odvoda, te izhajajo iz definicije: (af)′ = af′ in (f + g)′ = f′ + g′ ter f(g)′ = f′g′.

Podpoglavja:

• 5.3.1 Časovni odvodi in diferenciali v elektrotehniki

5.2 Kako analizirati prehodni pojav

5.3.1 Časovni odvodi in diferenciali v elektrotehniki