Iz e-ELEKTROTEHNIKA plus
| Vrstica 1: | Vrstica 1: | ||
[[Image:eele_foto_051.jpg|thumb|right|Fotografija 51]] | [[Image:eele_foto_051.jpg|thumb|right|Fotografija 51]] | ||
| - | [[Image: | + | [[Image:eele_foto_055.jpg|thumb|right|Fotografija 55]] |
Fizikalne količine so znanstveniki opredelili tako, da jih lahko '''merimo''' in '''računamo'''. Čeprav je sinusna oblika izmeničnih količin tista, s katero to naredimo najenostavneje, pa sl. 1.9 pove, da tako enostavno, kot z enosmernimi količinami, gotovo ne gre. Za računanje s sinusno količino pa najprej potrebujemo njen '''matematični zapis'''. Po podobi kroga enote (sl. 1.10) je na sl. 1.11 narisan krog, katerega polmer je določen s '''kazalcem''' »dolžine<ref>v merilu, npr. 100 V ≡ 1 cm oziroma 100 V/cm</ref>« '''''U'''''<sub>max</sub>. Če kazalec '''''U'''''<sub>max</sub> zavrtimo iz položaja po sl. 1.11 v nasprotni smeri urinega kazalca, bosta kot in kotu pripadajoča nasprotna kateta pravokotnega trikotnika naraščala. Pri kotu ''α'' = 90 ° doseže kateta »dolžino« '''''U'''''<sub>max</sub>, z nadaljnjim naraščanjem kota se začne njena dolžina zmanjševati … Grafični potek take odvisnosti katete od kota (sl. 1.12 b) ima sinusno obliko. Trenutno vrednost sinusne količine lahko torej zapišemo in računamo z enačbami, kot sta en. 1.2 in 1.3: | Fizikalne količine so znanstveniki opredelili tako, da jih lahko '''merimo''' in '''računamo'''. Čeprav je sinusna oblika izmeničnih količin tista, s katero to naredimo najenostavneje, pa sl. 1.9 pove, da tako enostavno, kot z enosmernimi količinami, gotovo ne gre. Za računanje s sinusno količino pa najprej potrebujemo njen '''matematični zapis'''. Po podobi kroga enote (sl. 1.10) je na sl. 1.11 narisan krog, katerega polmer je določen s '''kazalcem''' »dolžine<ref>v merilu, npr. 100 V ≡ 1 cm oziroma 100 V/cm</ref>« '''''U'''''<sub>max</sub>. Če kazalec '''''U'''''<sub>max</sub> zavrtimo iz položaja po sl. 1.11 v nasprotni smeri urinega kazalca, bosta kot in kotu pripadajoča nasprotna kateta pravokotnega trikotnika naraščala. Pri kotu ''α'' = 90 ° doseže kateta »dolžino« '''''U'''''<sub>max</sub>, z nadaljnjim naraščanjem kota se začne njena dolžina zmanjševati … Grafični potek take odvisnosti katete od kota (sl. 1.12 b) ima sinusno obliko. Trenutno vrednost sinusne količine lahko torej zapišemo in računamo z enačbami, kot sta en. 1.2 in 1.3: | ||
Trenutna redakcija s časom 10:45, 24. avgust 2010
![](javascript: loadPicture("Eele_foto_051.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_055.jpg", 1200);)
Fizikalne količine so znanstveniki opredelili tako, da jih lahko merimo in računamo. Čeprav je sinusna oblika izmeničnih količin tista, s katero to naredimo najenostavneje, pa sl. 1.9 pove, da tako enostavno, kot z enosmernimi količinami, gotovo ne gre. Za računanje s sinusno količino pa najprej potrebujemo njen matematični zapis. Po podobi kroga enote (sl. 1.10) je na sl. 1.11 narisan krog, katerega polmer je določen s kazalcem »dolžine[1]« Umax. Če kazalec Umax zavrtimo iz položaja po sl. 1.11 v nasprotni smeri urinega kazalca, bosta kot in kotu pripadajoča nasprotna kateta pravokotnega trikotnika naraščala. Pri kotu α = 90 ° doseže kateta »dolžino« Umax, z nadaljnjim naraščanjem kota se začne njena dolžina zmanjševati … Grafični potek take odvisnosti katete od kota (sl. 1.12 b) ima sinusno obliko. Trenutno vrednost sinusne količine lahko torej zapišemo in računamo z enačbami, kot sta en. 1.2 in 1.3:
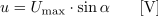
ali tudi
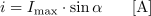
- Trenutna vrednost sinusne količine u, i, ... je določena s produktom maksimalne vrednosti sinusne količine Um, Im ... in sinusa trenutnega kota α.
Primer:
Izračunaj trenutne vrednosti sinusne napetosti, katere maksimalna vrednost ja 100 V, pri kotih 0 °, 30 °, 60 ° in 90 °.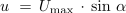
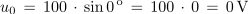
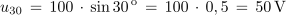
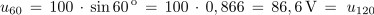
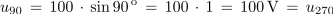
Kot α (°) ni enostavno merljiv ali kako drugače določljiv. Zato bomo v nadaljevanju enačbi 1.2 in 1.3 preuredili v obliko, ki kot α izraža z merljivima količinama – s frekvenco sinusne količine in časom.
Opombe
- ↑ v merilu, npr. 100 V ≡ 1 cm oziroma 100 V/cm
 1.1.3.2 Trenutna vrednost sinusne količine
| 1.1.3.4 Kako dobimo sinusno električno napetost?
|
