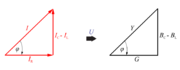Iz e-ELEKTROTEHNIKA plus
| Vrstica 1: | Vrstica 1: | ||
[[Image:eele_slika_3_2_16.svg|thumb|right|Slika 3.2.16: Trikotnik tokov in prevodnosti vzporedne vezave upora, tuljave in kondenzatorja]] | [[Image:eele_slika_3_2_16.svg|thumb|right|Slika 3.2.16: Trikotnik tokov in prevodnosti vzporedne vezave upora, tuljave in kondenzatorja]] | ||
[[Image:eele_foto_118.jpg|thumb|right|Fotografija 118]] | [[Image:eele_foto_118.jpg|thumb|right|Fotografija 118]] | ||
| + | [[Image:eele_foto_119.jpg|thumb|right|Fotografija 119]] | ||
| + | [[Image:eele_foto_120.jpg|thumb|right|Fotografija 120]] | ||
| + | [[Image:eele_foto_121.jpg|thumb|right|Fotografija 121]] | ||
| + | [[Image:eele_foto_122.jpg|thumb|right|Fotografija 122]] | ||
Iz kazalčnega diagrama na sl. 3.2.15 izrišemo '''trikotnik tokov''' (sl. 3.2.16 a), z deljenjem njegovih stranic s skupno količino elementov '''''U''''' pa dobimo trikotnik prevodnosti vezave (sl. 3.2.16 b). | Iz kazalčnega diagrama na sl. 3.2.15 izrišemo '''trikotnik tokov''' (sl. 3.2.16 a), z deljenjem njegovih stranic s skupno količino elementov '''''U''''' pa dobimo trikotnik prevodnosti vezave (sl. 3.2.16 b). | ||
Redakcija: 16:09, 24. avgust 2010
![](javascript: loadPicture("Eele_slika_3_2_16.svg", 800);)
![](javascript: loadPicture("Eele_foto_118.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_119.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_120.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_121.jpg", 1200);)
![](javascript: loadPicture("Eele_foto_122.jpg", 1200);)
Iz kazalčnega diagrama na sl. 3.2.15 izrišemo trikotnik tokov (sl. 3.2.16 a), z deljenjem njegovih stranic s skupno količino elementov U pa dobimo trikotnik prevodnosti vezave (sl. 3.2.16 b).
- Toki in prevodnosti izmeničnega kroga z vzporedno vezavo upora, tuljave in kondenzatorja tvorijo pravokotna trikotnika.
- Toke in prevodnosti vzporedne vezave upora, tuljave in kondenzatorja seštevamo geometrično.
Po pravilih za računanje v pravokotnem trikotniku lahko zapišemo:
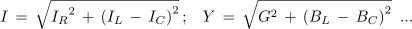
ali tudi
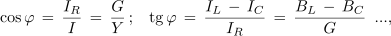
kar pri treh znanih količinah trikotnika omogoča računanje četrte količine.
V medsebojnem odnosu kapacitivne in induktivne prevodnosti in posledično tudi tokov vzporedne vezave elementov (sl. 3.2.15) obstajajo tri možnosti:
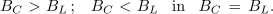
V vseh treh primerih admitanco vezave izračunamo na enak, zgoraj navedeni način. Zanimiv primer nastopi v primeru enakosti:
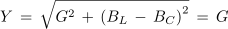
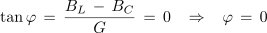
- Admitanca vzporedne vezave upora, tuljave in kondenzatorja je v primeru enakosti njunih jalovih prevodnosti najmanjša. Enaka je le delovni prevodnosti in ne povzroča faznega premika med napetostjo in tokom izvora.
V primeru enakosti induktivne in kapacitivne prevodnosti ima vzporedni vezava upora, tuljave in kondenzatorja, podobno kot zaporedna vezava, še druge zanimive lastnosti, ki pa jih bomo obravnavali pri resonančnih pojavih.
Primera:
Primer:
1. Vzporedna vezava upora z upornostjo 750 Ω, tuljave z induktivnostjo 20 mH in kondenzatorja s kapacitivnostjo 100 nF je priključena na izvor sinusne napetosti frekvence 5 kHz. Izračunaj admitanco, impedanco ter fazni kot, ki ga vezava povzroča v električnem krogu.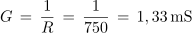
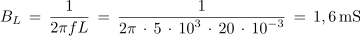
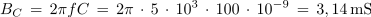
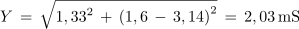
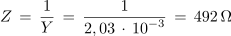
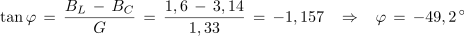
Primer:
2. Izračunaj kapacitivnost kondenzatorja, ki ga moramo vezati vzporedno z vzporedno vezanima uporom z upornostjo 2,7 kΩ in tuljavo z induktivnostjo 200 μH, če želimo, da bo vezava pri krožni frekvenci 2,5 • 106 s-1 povzročala zaostajanje toka za napetostjo za 30 º.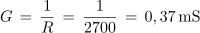
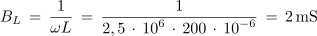
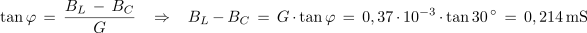
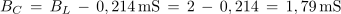
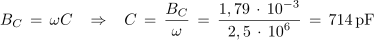
 3.2.4.1 Kazalčni diagram napetosti in tokov
| 3.2.4.3 Vzporedna RLC vezava (interaktivna simulacija)
|
