7.3.1 Zaporedni električni nihajni krog

Iz e-ELEKTROTEHNIKA plus

Redakcija iz 15:36, 12. maj 2010 od Latac (Pogovor | prispevki)

(prim) ← Starejša redakcija | poglejte trenutno redakcijo (prim) | Novejša redakcija → (prim)

Zaporedni RLC nihajni krog je v osnovi izmenični krog z vsemi lastnostmi, ki smo jih spoznali pri obravnavi kroga z zaporedno vezavo upora, tuljave in kondenzatorja.

Poskus 7.3.1:

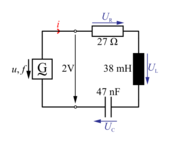
Zaporedno vezavo upora z upornostjo 27 Ω, tuljave z induktivnostjo 38 mH in upornostjo navitja 23 Ω ter kondenzatorja s kapacitivnostjo 47 nF priključimo na generator sinusne napetosti ≈ 2 V, katere frekvenco lahko spreminjamo (sl. 7.3.4).

Slika 7.3.4

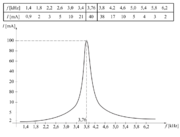
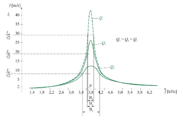
Pri stalni napetosti izvora 2 V postopoma povečujmo frekvenco napetosti od npr. 1000 do 10000 Hz in merimo tok v krogu. Dobili bomo vrednosti, ki jih grafično ponazarja slika 7.3.5.

Slika 7.3.5: Frekvenčni potek toka v zaporednem RLC nihajnem krogu

Pri določeni frekvenci (≈ 3,76 kHz) je tok v nihajnem krogu velik, pri višjih in nižjih frekvencah pa je bistveno manjši.

Praktično enak frekvenčni potek toka bi dobili z računanjem impedanc vezave za posamezne frekvence in pripadajočih tokov po Ohmovem zakonu.

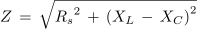
in

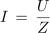
Pri tem bi ugotovili, da sta pri frekvenci 3,76 kHz reaktanci X_L in X_C praktično enaki, impedanca najmanjša in enaka le ohmski upornosti R in tok, tudi računsko, največji:

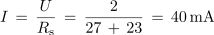
Pri določeni frekvenci napetosti izvora je vsiljeno nihanje energije v nihajnem krogu bistveno intenzivnejše in tok večji kot pri drugih frekvencah.

Pojav je podoben, kot ga poznamo pri drugih nihanjih. Tudi neuravnoteženo kolo avtomobila povzroča pri določeni hitrosti (številu vrtljajev kolesa) bistveno močnejše tresenje avtomobila kot pri večji ali manjši hitrosti. Vsiljeno nihanje mehanskih sistemov s frekvenco, ki je enaka frekvenci lastnega nihanja sistema, lahko vodi tudi v razpad sistema. Popolnoma nov, kilometer dolg viseči most v ameriški zvezni državi Washington, so močni sunki vetra leta 1940 pognali v lastno nihanje, ki je most spektakularno sesulo v reko.

Resonančna frekvenca

Frekvenco vsiljenega nihanja, pri kateri je amplituda nihanja energije v zaporednem nihajnem krogu bistveno večja kot pri drugih frekvencah, imenujemo resonančna^[1] frekvenca (f_r).

Resonančno frekvenco izračunamo iz enakosti reaktanc nihajnega kroga pri resonančni frekvenci:

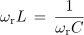
oziroma

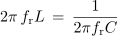
in od tod

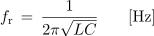
Resonančna frekvenca zaporednega nihajnega kroga je obratno sorazmerna z geometrično sredino induktivnosti L in kapacitivnosti kroga C (√LC).

Resonančna frekvenca vsiljenega nihanja je enaka frekvenci lastnega nihanja nedušenega nihajnega kroga, enačbo za računanje frekvence lastnega oziroma vsiljenega resonančnega nihanja pa imenujemo Thomsonova^[2] enačba.

Izračunajmo resonančno frekvenco nihajnega kroga iz poskusa 7.3.1:

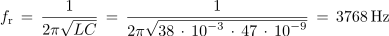
Za zaporedni nihajni krog pri f = f_r torej velja:

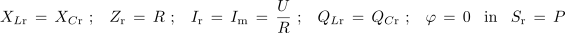
Kakovost zaporednega nihajnega kroga (Q)

Spoznali smo, da se pri vsiljenem nihanju pri resonančni frekvenci izmenjuje energija med kondenzatorjem in tuljavo z največjo intenzivnostjo in da je za vzdrževanje vsiljenega nihanja potrebno kriti izgube energije v realnem kondenzatorju in tuljavi z dovajanjem energije iz izvora napetosti. Čim kakovostnejša sta kondenzator in tuljava, tem manjše bodo izgube in manj energije bo potrebno za vzdrževanje nihanja energije v nihajnem krogu.

Razmerje moči nihanja med kondenzatorjem in tuljavo pri resonančni frekvenci (Q_Lr = Q_Cr) in izgubne moči (P) določa kakovost zaporednega nihajnega kroga.

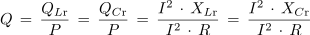
oziroma po ureditvi

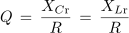
Kakovost zaporednega nihajnega kroga je premo sorazmerna z reaktancama nihajnega kroga pri resonančni frekvenci in obratno sorazmerna z izgubno upornostjo tuljave in kondenzatorja.

Primer:

Kolikšna je kakovost zaporednega nihajnega kroga, v katerem je induktivnost tuljave 20 mH in ohmska upornost ovojev tuljave 10 Ω pri resonančni frekvenci 5 kHz? Izgube v kondenzatorju in izvoru so v primerjavi s tuljavo dovolj majhne, da jih lahko zanemarimo.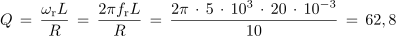

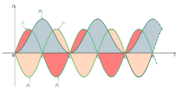
Rešitev

V danem primeru je moč na kondenzatorju in tuljavi 62,8 krat večja od moči, ki jo izvor napetosti potrebuje za vzdrževanje nihanja, kar je primer relativno dobre kakovosti nihajnega kroga. Sl. 7.3.6 pa prikazuje časovni potek moči in energije v nihajnem krogu slabe kakovosti.

Slika 7.3.6: Časovni potek moči v nihajnem krogu slabe kakovosti

Frekvenčna karakteristika toka zaporednega nihajnega kroga

Iz oblike frekvenčnega poteka (karakteristike) toka lahko razberemo še eno, v bistvu najpomembnejšo lastnost zaporednega nihajnega kroga:

Zaporedni nihajni krog prepušča zelo dobro tok resonančne frekvence in frekvenc, ki so resonančni blizu, toke višjih in nižjih frekvenc pa močno duši.

Če bi namesto izvora čiste sinusne napetosti na nihajni krog priključili izvor iz množice napetosti različnih frekvenc sestavljene napetosti, bi v nihajnem krogu imeli predvsem tok resonančne frekvence in toke, katerih frekvence so blizu resonančni.

Zaporedni nihajni krog je pasovno prepustni frekvenčni filter.
Lastnost nihajnega kroga, da iz množice tokov različnih frekvenc »izbira« in prepušča toke le določenih frekvenc, imenujemo selektivnost^[3].
Čim ožja je frekvenčna karakteristika in čim strmejši so njeni boki, tem večja je selektivnosti zaporednega nihajnega kroga.

Pravkar ugotovljena lastnost nihajnega kroga omogoča radijskim in TV sprejemnikom, da iz množice signalov, ki jih sprejema antena, izločijo le želenega. Sprejemniki z boljšo selektivnostjo bolje ločijo želeni signal od neželenega (ki ga ne želimo poslušati).

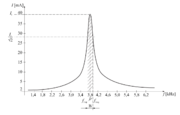
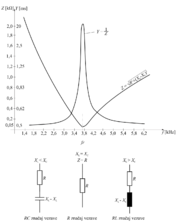
Področje frekvenc, katerih toke zaporedni nihajni krog dobro prevaja, imenujemo prepustni frekvenčni pas nihajnega kroga (B)^[4] (slika 7.3.7).

Bolj točno je prepustni frekvenčni pas zaporednega nihajnega kroga določen na naslednji način:

Prepustni frekvenčni pas zaporednega nihajnega kroga je območje frekvenc, v katerem moč v nihajnem krogu ne pade pod P_r ⁄ 2 oziroma tok v nihajnem krogu ni manjši od I_r ⁄ √2.
Širina prepustnega frekvenčnega pasu B je določena z razliko mejnih frekvenc prepustnega frekvenčnega pasu f_mzg in f_msp.

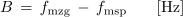
Slika 7.3.7: Frekvenčni prepustni pas nihajnega kroga (prepustnega filtra)

Enačbo za neposredno računanje širine frekvenčnega pasu B dobimo iz razmerja tokov pri resonančni in mejni frekvenci. Pot do enačbe je nekoliko zahtevnejša, zato napišimo le rezultat:

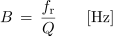
Širina prepustnega frekvenčnega pasu zaporednega nihajnega kroga je premo sorazmerna z resonančno frekvenco in obratno sorazmerna s faktorjem kakovosti nihajnega kroga.

Oblika frekvenčne karakteristike ni ravno simetrična glede na resonančno frekvenco, toda za faktor kakovosti Q > 10 velja, da je prepustni pas glede na resonančno frekvenco praktično simetričen.

Primer:

Izračunaj širino frekvenčnega prepustnega pasu B, mejni frekvenci f₁ in f₂ ter toke pri resonančni in mejnih frekvencah za nihajni krog iz poskusa 7.3.1 (f_r = 3768 Hz, R_t = 23 Ω).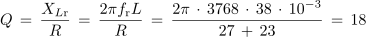

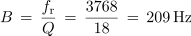
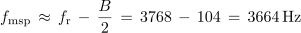
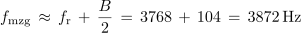
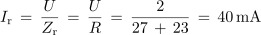
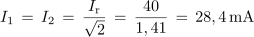
Rešitev

Pred naslednjim poskusom izračunajmo faktorje kakovosti nihajnega kroga iz poskusa 7.3.1 še pri upornosti upora 56 Ω in 150 Ω. V obeh primerih upoštevajmo ohmsko upornost tuljave (R_t = 23 Ω).

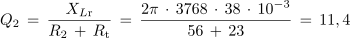
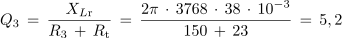
Z naraščajočo delovno upornostjo kakovost nihajnega kroga pada.

Poskus 7.3.2:

Ponovimo poskus 7.3.1 tako, da namesto upora z upornostjo 27 Ω vključimo v krog najprej upor z upornostjo 56 Ω in potem še upor z upornostjo 150 Ω, torej tako, da pri stalni napetosti in frekvenci zmanjšujemo kakovost nihajnega kroga. Rezultat meritev prikazuje grafično slika 7.3.8.

Slika 7.3.8: Vpliv kakovosti na obliko frekvenčne karakteristike toka zaporednega nihajnega kroga

Večja ohmska upornost povzroči manjši resonančni tok in širši prepustni pas nihajnega kroga.

Čim večja je kakovost nihajnega kroga, tem večji je resonančni tok, tem ožji je frekvenčni prepustni pas in tem boljša je selektivnost zaporednega nihajnega kroga.

Frekvenčna karakteristika impedance zaporednega nihajnega kroga

Frekvenčno karakteristiko toka (slika 7.3.7) smo dobili pri konstantni napetosti izvora v krogu, zato bi pripadajočo frekvenčno karakteristiko impedance ali admitance lahko dobili že po Ohmovem zakonu:

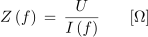
in

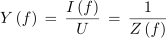
Slika 7.3.9: Frekvenčni karakteristiki polne upornosti in prevodnosti zaporednega nihajnega kroga

Slika 7.3.9 pravzaprav ne prinaša novosti – le nazorneje prikazuje spoznanja o lastnostih zaporedne vezave upora, tuljave in kondenzatorja v izmeničnem krogu. »Novost« je predvsem to, da nihajni krogi koristijo lastnosti zaporednega RLC kroga predvsem pri resonančni frekvenci.

Napetostna resonanca

Poskus 7.3.3:

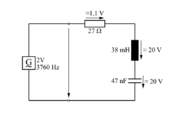
V nihajnem krogu iz poskusa 7.3.1 izmerimo napetosti v krogu pri resonančni frekvenci (sl. 7.3.10).

Slika 7.3.10

Padec napetosti na delovni upornosti kroga (če upoštevamo tudi izgubni upornosti tuljave in kondenzatorja) je približno enaka napetosti izvora.
Padca napetosti na tuljavi in kondenzatorju sta enaki in veliko večji od napetosti izvora.

Kazalčni diagram izmeničnega kroga z zaporedno vezavo upora, tuljave in kondenzatorja^[5] dopušča možnost večjih napetosti na tuljavi in kondenzatorju od napetosti izvora, zato si oglejmo le odvisnost te razlike. Pri znanih dejstvih

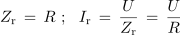
in

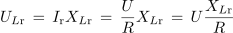
ter z upoštevanjem

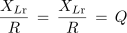
dobimo

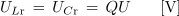
Napetosti na tuljavi in kondenzatorju v zaporednem nihajnem krogu sta pri resonančni frekvenci Q - krat večji od napetosti izvora ali napetosti na delovni upornosti kroga.
Zaradi pojava ojačevanja napetosti imenujemo resonanco zaporednega nihajnega kroga napetostna resonanca.

Primer:

Zaporedni nihajni krog ima pri resonančni frekvenci 5 kHz reaktanci X_L = X_C = 100 Ω in izgubno delovno upornost R = 2 Ω. Priključen je na generator izmenične napetosti 10 V / 5 kHz. Določi tok in moč delovanja izvora, fazni kot, padce napetosti, kakovost, širino prepustnega frekvenčnega pasu ter tok in moč izvora pri mejnih frekvencah nihajnega kroga.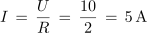

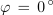
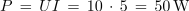
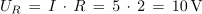
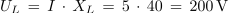
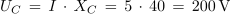
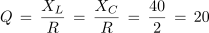
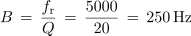
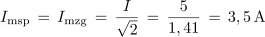
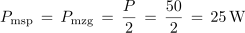
Rešitev

Napetostno resonanco koristno uporabljamo na področju elektronike, predvsem v radijski, TV in krmilni tehniki. Na področju energetike, kjer so večje napetosti in moči izvorov, moramo biti pri konstrukciji električnih naprav in sistemov previdni. Delovanje le-teh na frekvencah, ki so blizu ali enake njihovi resonančni frekvenci, je lahko vzrok nepričakovano visokih napetosti, nevarnih za merilnike, izolacijo in tudi za človeka.