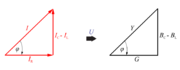Iz e-ELEKTROTEHNIKA plus
| Vrstica 1: | Vrstica 1: | ||
[[Image:eele_slika_3_2_13.svg|thumb|right|Slika 3.2.13 ]] | [[Image:eele_slika_3_2_13.svg|thumb|right|Slika 3.2.13 ]] | ||
[[Image:eele_slika_3_2_2.svg|thumb|right|Slika 3.2.2: Upornost sestavljenega izmeničnega kroga]] | [[Image:eele_slika_3_2_2.svg|thumb|right|Slika 3.2.2: Upornost sestavljenega izmeničnega kroga]] | ||
| - | |||
| - | |||
| - | |||
<poskus> | <poskus> | ||
| Vrstica 23: | Vrstica 20: | ||
== Kazalčni diagram napetosti in tokov == | == Kazalčni diagram napetosti in tokov == | ||
| - | + | [[Image:eele_slika_3_2_14.svg|thumb|right|Slika 3.2.14: Kazalčni diagram vzporednega RLC kroga]] | |
| + | [[Image:eele_slika_3_2_15.svg|thumb|right|Slika 3.2.15: Kazalčni diagrami vzporednega izmeničnega kroga]] | ||
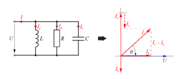
Skupna količina elementom kroga je napetost ''U'', na že znani način pa dobimo kazalčni diagram, ki ga prikazuje sl.3.2.14: | Skupna količina elementom kroga je napetost ''U'', na že znani način pa dobimo kazalčni diagram, ki ga prikazuje sl.3.2.14: | ||
| Vrstica 58: | Vrstica 56: | ||
== Trikotnik tokov in prevodnosti == | == Trikotnik tokov in prevodnosti == | ||
| - | + | [[Image:eele_slika_3_2_16.svg|thumb|right|Slika 3.2.16: Trikotnik tokov in prevodnosti vzporedne vezave upora, tuljave in kondenzatorja]] | |
Iz kazalčnega diagrama na sl. 3.2.15 izrišemo '''trikotnik tokov''' (sl. 3.2.16 a), z deljenjem njegovih stranic s skupno količino elementov '''''U''''' pa dobimo trikotnik prevodnosti vezave (sl. 3.2.16 b). | Iz kazalčnega diagrama na sl. 3.2.15 izrišemo '''trikotnik tokov''' (sl. 3.2.16 a), z deljenjem njegovih stranic s skupno količino elementov '''''U''''' pa dobimo trikotnik prevodnosti vezave (sl. 3.2.16 b). | ||
Redakcija: 09:51, 11. maj 2010
![](javascript: loadPicture("Eele_slika_3_2_13.svg", 886);)
![](javascript: loadPicture("Eele_slika_3_2_2.svg", 1248);)
Poskus 2.2.4:
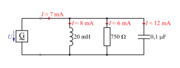
Vzporedno vezavo upora z upornostjo 750 Ω, tuljave z induktivnostjo 20 mH in kondenzatorja s kapacitivnostjo 0,1 µF priključimo na napetost 4,5 V/4,4 kHz (sl. 3.2.13)
Izmerimo efektivne toke IR, IL, IC in I ter preverimo izmerjeno z zakonom tokovnega vozlišča:
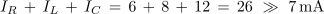
Aritmetična vsota efektivnih tokov je v danem primeru precej večja od efektivnega toka izvora. Nekaj podobnega smo ugotovili tudi pri zaporedni vezavi vseh treh elementov v poskusu 3.2.2, le da smo takrat imeli opravka z napetostmi.
Kazalčni diagram napetosti in tokov
![](javascript: loadPicture("Eele_slika_3_2_14.svg", 956);)
![](javascript: loadPicture("Eele_slika_3_2_15.svg", 1378);)
Skupna količina elementom kroga je napetost U, na že znani način pa dobimo kazalčni diagram, ki ga prikazuje sl.3.2.14:
- V vzporednem izmeničnem krogu z uporom, tuljavo in kondenzatorjem sta kazalca tokov tuljave in kondenzatorja nasprotno usmerjena in pravokotna na kazalec toka skozi upor.
- Toka tuljave in kondenzatorja sta v protifazi.
- Efektivni tok izvora je enak geometrični vsoti efektivnih tokov upora, tuljave in kondenzatorja.
Razmerje tokov tuljave in kondenzatorja je odvisno od razmerja induktivne in kapacitivne upornosti. Možni so trije splošni primeri:
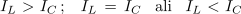
Kazalčne diagrame za navedene tri primere kaže primerjalno slika 3.2.15 a, b in c.
- V izmeničnem krogu z vzporedno vezavo upora, tuljave in kondenzatorja tok lahko prehiteva, zaostaja ali pa je v fazi z napetostjo izvora (podobno kot pri zaporedni vezavi istih elementov).
- Vzporedna vezava upora, tuljave in kondenzatorja ima lahko značaj in lastnosti vzporedne vezave upora in tuljave ali upora in kondenzatorja ali samo upora.
Vzporedna vezava upora, tuljave in kondenzatorja povzroča v izmeničnem krogu fazni kot med - 90 º in + 90 º.
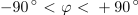
Trikotnik tokov in prevodnosti
![](javascript: loadPicture("Eele_slika_3_2_16.svg", 800);)
Iz kazalčnega diagrama na sl. 3.2.15 izrišemo trikotnik tokov (sl. 3.2.16 a), z deljenjem njegovih stranic s skupno količino elementov U pa dobimo trikotnik prevodnosti vezave (sl. 3.2.16 b).
- Toki in prevodnosti izmeničnega kroga z vzporedno vezavo upora, tuljave in kondenzatorja tvorijo pravokotna trikotnika.
- Toke in prevodnosti vzporedne vezave upora, tuljave in kondenzatorja seštevamo geometrično.
Po pravilih za računanje v pravokotnem trikotniku lahko zapišemo:
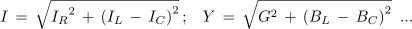
ali tudi
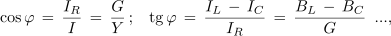
kar pri treh znanih količinah trikotnika omogoča računanje četrte količine.
V medsebojnem odnosu kapacitivne in induktivne prevodnosti in posledično tudi tokov vzporedne vezave elementov (sl. 3.2.15) obstajajo tri možnosti:
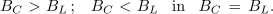
V vseh treh primerih admitanco vezave izračunamo na enak, zgoraj navedeni način. Zanimiv primer nastopi v primeru enakosti:
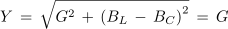
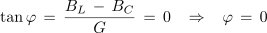
- Admitanca vzporedne vezave upora, tuljave in kondenzatorja je v primeru enakosti njunih jalovih prevodnosti najmanjša. Enaka je le delovni prevodnosti in ne povzroča faznega premika med napetostjo in tokom izvora.
V primeru enakosti induktivne in kapacitivne prevodnosti ima vzporedni vezava upora, tuljave in kondenzatorja, podobno kot zaporedna vezava, še druge zanimive lastnosti, ki pa jih bomo obravnavali pri resonančnih pojavih.
Primera:
Primer:
1. Vzporedna vezava upora z upornostjo 750 Ω, tuljave z induktivnostjo 20 mH in kondenzatorja s kapacitivnostjo 100 nF je priključena na izvor sinusne napetosti frekvence 5 kHz. Izračunaj admitanco, impedanco ter fazni kot, ki ga vezava povzroča v električnem krogu.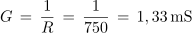
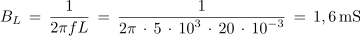
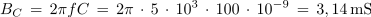
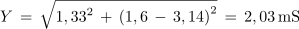
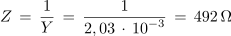
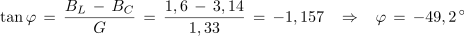
Primer:
2. Izračunaj kapacitivnost kondenzatorja, ki ga moramo vezati vzporedno z vzporedno vezanima uporom z upornostjo 2,7 kΩ in tuljavo z induktivnostjo 200 μH, če želimo, da bo vezava pri krožni frekvenci 2,5 • 106 s-1 povzročala zaostajanje toka za napetostjo za 30 º.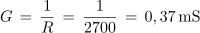
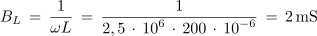
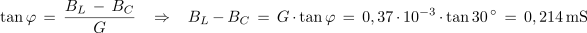
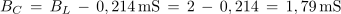
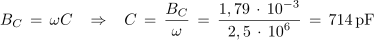
Podpoglavja:
- 3.2.4.1 Kazalčni diagram napetosti in tokov
- 3.2.4.2 Trikotnik tokov in prevodnosti.
- 3.2.4.3 Vzporedna RLC vezava (interaktivna simulacija)
 3.2.3.2 Trikotnik tokov in prevodnosti
| 3.2.4.1 Kazalčni diagram napetosti in tokov
|
