|
|
| (5 intermediate revisions not shown) |
| Vrstica 1: |
Vrstica 1: |
| - | [[Image:eele_slika_5_2_1.svg|thumb|right|Slika 5.2.1: Vezave navitij in tuljav v izmeničnih krogih]]
| |
| - | [[Image:eele_slika_5_2_2.svg|thumb|right|Slika 5.2.2: Magnetno sklenjeni tuljavi]]
| |
| - | [[Image:eele_slika_5_2_3.svg|thumb|right|Slika 5.2.3: Medsebojne lege tuljave brez medsebojne induktivnosti]]
| |
| - | [[Image:eele_slika_5_2_4.svg|thumb|right|Slika 5.2.4: Izmenični krog z zaporednima tuljavama in medsebojno induktivnostjo]]
| |
| - | [[Image:eele_slika_5_2_5.svg|thumb|right|Slika 5.2.5: lstosmiselna a) in b) ter protismiselna c) in d) magnetna povezava tuljav]]
| |
| - | [[Image:eele_slika_5_2_6.svg|thumb|right|Slika 5.2.6: Vzporedna vezava tuljav z medsebojno induktivnostjo]]
| |
| | | | |
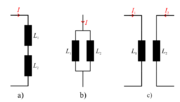
| | Tuljave kot elektronske elemente redkeje vežemo zaporedno ali vzporedno. Navitja elektroenergetskih strojev in naprav pa so pogosti primeri različnim vezavam navitij (sl. 5.2.1), transformatorski sklopi tuljav (sl. 5.2.1 c) pa so pogosti tudi na področju elektronike. | | Tuljave kot elektronske elemente redkeje vežemo zaporedno ali vzporedno. Navitja elektroenergetskih strojev in naprav pa so pogosti primeri različnim vezavam navitij (sl. 5.2.1), transformatorski sklopi tuljav (sl. 5.2.1 c) pa so pogosti tudi na področju elektronike. |
| | | | |
| | | | |
| - | Slika 5.2.1: Vezave navitij in tuljav v izmeničnih krogih | + | [[Image:eele_slika_5_2_1.svg|thumb|right|Slika 5.2.1: Vezave navitij in tuljav v izmeničnih krogih]] |
| - | | + | |
| | | | |
| | V navedenih in podobnih primerih obstaja velika verjetnost, da se magnetni pretok ene tuljave delno sklene tudi skozi ovoje druge tuljave. | | V navedenih in podobnih primerih obstaja velika verjetnost, da se magnetni pretok ene tuljave delno sklene tudi skozi ovoje druge tuljave. |
| Vrstica 22: |
Vrstica 15: |
| | | | |
| | | | |
| - |
| |
| - | == Medsebojna induktivnost tuljav ==
| |
| - |
| |
| - |
| |
| - | Izhajajmo iz predpostavke, da se magnetna pretoka tuljav 1 in 2 (slika 5.2.2) deloma skleneta tudi skozi ovoje druge tuljave.
| |
| - |
| |
| - |
| |
| - | Slika 5.2.2: Magnetno sklenjeni tuljavi
| |
| - |
| |
| - |
| |
| - | Celotni magnetni pretok prve tuljave označimo s ''Ф''<sub>1</sub> druge s ''Ф''<sub>2</sub>, del magnetnega pretoka prve tuljave, ki se sklene tudi skozi ovoje druge tuljave, s ''Ф''<sub>12</sub> in del ''Ф''<sub>2</sub>, ki se sklene tudi skozi ovoje prve tuljave, s ''Ф''<sub>21</sub>. Delna magnetna pretoka potem lahko zapišemo v obliki:
| |
| - |
| |
| - |
| |
| - | <latex>{\Phi _{12}}\, =\, {k_{12}} \,\cdot\, {\Phi _1}</latex>
| |
| - |
| |
| - | <latex>{\Phi _{21}}\, =\, {k_{21}} \,\cdot \,{\Phi _2}</latex>
| |
| - |
| |
| - |
| |
| - | Faktorja k<sub>12</sub> in k<sub>21</sub> sta '''sklopna faktorja''' tuljav.
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Sklopni faktor dveh tuljav je število, ki pove, kolikšen del magnetnega pretoka ene tuljave se sklene tudi skozi ovoje druge tuljave.
| |
| - | *Teoretično možne vrednosti sklopnih faktorjev so med '''0''' in '''1'''.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | Do končnih enačb, ki povedo nekaj več o lastnostih in medsebojnih vplivih magnetno sklenjenih tuljav,
| |
| - | je relativno zahtevna pot. Ker se izven razvoja električnih naprav v praksi s tovrstnimi računi praktično
| |
| - | ne bomo ukvarjali, se s končnimi enačbami in lastnostmi magnetno sklenjenih tuljav le seznanimo.
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | Razmerje med magnetnim sklepom<ref>Osnove elektrotehnike 1, str. 242</ref> sklenjenega magnetnega pretoka v drugi tuljavi in električnim tokom v prvi tuljavi, ki ga ustvarja, imenujemo '''medsebojna induktivnost''' ('''''M'''''). </pomembno>
| |
| - |
| |
| - |
| |
| - | <latex>{M\, =\, k\sqrt {{L_1}{L_2}} }|||(H)</latex>
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Medsebojna induktivnost dveh tuljav '''''M''''' je premo sorazmerna s '''sklopnim faktorjem'''<ref><latex>k\, =\, \sqrt {{k_{12}}{k_{21}}} </latex></ref> tuljav '''''k''''' in '''srednjo geometrično''' vrednostjo induktivnosti tuljav.</pomembno>
| |
| - |
| |
| - |
| |
| - | Medsebojna induktivnost ''M'' ima enake fizikalne lastnosti kot induktivnost tuljave, zato povzroča '''indukcijo napetosti''' v dveh sosednjih tuljavah, ki je lahko koristna ali moteča. Med najbolj pogostimi koristnimi primeri uporabe medsebojne induktivnosti je npr. električni '''transformator''', med motečimi pa je gotovo škodljiv vpliv magnetnih polj '''energetskih vodnikov''' na občutljive '''elektronske sisteme'''.
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Škodljive primere medsebojnih induktivnosti pogosto imenujemo '''parazitne''' induktivnosti.</pomembno>
| |
| - |
| |
| - |
| |
| - | Medsebojne induktivnosti tuljav ni (''M'' ≈ 0), le v primerih, če sta tuljavi vsaka zase v zaprtem '''feromagnetnem jedru''' ali če sta njuni osi med seboj '''pravokotni''' (slika 5.2.3) ali če sta med seboj dovolj '''oddaljeni'''.
| |
| - |
| |
| - |
| |
| - | Slika 5.2.3: Medsebojne lege tuljave brez medsebojne induktivnosti
| |
| - |
| |
| - |
| |
| - |
| |
| - | == Induktivnost zaporedne vezave tuljav ==
| |
| - |
| |
| - |
| |
| - | V primeru magnetne povezave tuljav moramo v enačbi napetostne zanke električnega kroga z zaporedno vezavo tuljav (sl. 5.2.4) poleg napetosti lastne indukcije tuljav (''U<sub>L</sub>'' = ''I'' • ''X<sub>L</sub>'') upoštevati tudi napetosti '''medsebojne indukcije'''.
| |
| - |
| |
| - |
| |
| - | Slika 5.2.4: Izmenični krog z zaporednima tuljavama in medsebojno induktivnostjo
| |
| - |
| |
| - |
| |
| - | V zaporedno vezanih tuljavah ima tok sicer isto smer, toda glede na smer navijanja tuljav se sklenjena magnetna pretoka lastnemu pretoku tuljave lahko '''prištevata''' ali '''odštevata'''.
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Napetost medsebojne indukcije ima '''enako''' ali '''nasprotno''' smer napetosti lastne indukcije tuljave.
| |
| - | *Razlikujemo '''pozitivni''' in '''negativni''' medsebojni magnetni sklep tuljav
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | Enačba napetostne zanke izmeničnega kroga z zaporednima tuljavama (slika 5.2.4) se potem glasi:
| |
| - |
| |
| - |
| |
| - | <latex>U\, =\, {U_{L1}}\, +\, {U_{1M}}\, +\, {U_{L2}}\, + \,{U_{2M}}\, =\, I\, \cdot \,\omega {L_1} \,\pm \,I\, \cdot \,\omega M \,+\, I \,\cdot \,\omega {L_2} \,\pm \,I \,\cdot\, \omega M</latex>
| |
| - | <latex> \,\,\,=\, I\, \cdot\, \omega \left( {{L_1} \,+\, {L_2} \,\pm\, 2M} \right)</latex>
| |
| - | <latex> \,\,\,=\, I\, \cdot\, \omega L</latex>
| |
| - |
| |
| - |
| |
| - | ''L'' je skupna oziroma nadomestna induktivnost zaporedne vezave dveh tuljav, zato lahko zapišemo:
| |
| - |
| |
| - |
| |
| - | <latex>{L\, =\, {L_1} \,+ \,{L_2}\, \pm\, 2M}|||(H)</latex>
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Skupna induktivnost zaporedno vezanih in '''magnetno sklenjenih tuljav''' je enaka vsoti induktivnosti tuljav, '''povečani''' ali '''zmanjšani''' za '''dvakratno medsebojno induktivnost'''.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | Če se z drugo tuljavo sklenjena magnetna pretoka ''Ф''<sub>12</sub> in ''Ф''<sub>21</sub> prištevata lastnima magnetnima pretokoma tuljav ''Ф''<sub>1</sub> in ''Ф''<sub>2</sub>, sta tuljavi povezani magnetno '''istosmiselno''', sicer pa '''protismiselno'''. Smiselnost magnetne povezave tuljav označujemo s '''pikami''' ob simbolih tuljav (slika 5.2.5).
| |
| - |
| |
| - |
| |
| - | Slika 5.2.5: lstosmiselna a) in b) ter protismiselna c) in d) magnetna povezava tuljav
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Če električna toka vstopata v tuljavi na označenih koncih, sta tuljavi magnetno povezani '''istosmiselno''', sicer pa '''protismiselno'''.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - | Zadnja ugotovitev omogoča fizikalno razlago, zakaj '''bifilarno'''<ref>Dvojno navitje, ki omogoča tok v ovojih v nasprotnih smereh – navitje brez magnetnega polja</ref> navitje žičnih uporov nima induktivnosti. Zaradi k ≈ 1 je magnetni sklep sklenjenega magnetnega pretoka popoln in je medsebojna induktivnost zaradi ''L''<sub>1</sub> = ''L''<sub>2</sub> = ''L''<sub>t</sub> kar
| |
| - |
| |
| - |
| |
| - | <latex>M \,=\, k\sqrt {{L_1}{L_2}} \, =\, {L_{\rm{t}}}</latex>
| |
| - |
| |
| - | in zaradi protismiselne vezave tuljav
| |
| - |
| |
| - | <latex>L \,=\, {L_{\rm{t}}}\, +\, {L_{\rm{t}}}\, -\, 2{L_{\rm{t}}} \,=\, 0</latex>
| |
| - |
| |
| - |
| |
| - | Če sta zaporedno vezani tuljavi na '''veliki''' medsebojni '''razdalji''' ali sta v zaprtih '''feromagnetnih jedrih''' ali pa sta osi tuljav med seboj '''pravokotni''', medsebojne induktivnosti tuljav '''''M''''' '''ni''' (''M'' ≈ 0). V tem primeru je skupna induktivnost tuljav kar
| |
| - |
| |
| - |
| |
| - | <latex>{L \,=\, {L_1} \,+\, {L_2}}|||(H)</latex>
| |
| - |
| |
| - |
| |
| - | <pomembno>
| |
| - | *Skupna induktivnost '''zaporedno''' vezanih in magnetno '''nepovezanih''' tuljav je enaka '''vsoti''' induktivnosti tuljav.
| |
| - | </pomembno>
| |
| - |
| |
| - |
| |
| - |
| |
| - | == Induktivnost vzporedne vezave tuljav ==
| |
| - |
| |
| - |
| |
| - | Pot do izrazov za skupno induktivnost vzporedno vezanih tuljav (slika 5.2.6) je podobna kot pri zaporedni vezavi, zato napišimo le končne oblike le-teh:
| |
| - |
| |
| - |
| |
| - | Slika 5.2.6: Vzporedna vezava tuljav z medsebojno induktivnostjo
| |
| - |
| |
| - |
| |
| - | <latex>L\, =\, \frac{{L_1}{L_1} \,- \,{M^2}}{{L_1} \,+\, {L_1}\, \pm \,2M},</latex>
| |
| - |
| |
| - |
| |
| - | pri čemer velja »- 2''M''« v imenovalcu izraza za '''istosmiselno''', »+ 2''M''« pa za '''protismiselno''' magnetno povezavo tuljav. Če pa je medsebojna induktivnost tuljav '''zanemarljiva''' (''k'' ≈ 0 in ''M'' ≈ 0), dobimo:
| |
| - |
| |
| - |
| |
| - | <latex>{L\, =\, \frac{{L_1}{L_1}}{{L_1}\, +\, {L_1}}}|||(H)</latex>
| |
| - |
| |
| - |
| |
| - | '''Primera:'''
| |
| - |
| |
| - | <primer>
| |
| - | 1. Izračunaj induktivnost zaporedno vezanih tuljav z induktivnostmi ''L''<sub>1</sub> = 200 mH in ''L''<sub>2</sub> = 300 mH, in sicer: a) tuljavi nista magnetno sklenjeni in b) tuljavi sta negativno magnetno sklenjeni s ''k'' = 0,2.|||
| |
| - | <latex>L \,=\, {L_1} \,+\, {L_2}\, =\, 200 \,+\, 300\, =\, 500{\rm{\,mH}}</latex>
| |
| - |
| |
| - | <latex>M \,=\, k\sqrt {{L_1}{L_2}}\, = \,{\rm{0,2}}\sqrt {200 \,\cdot \,300} \, =\, 49{\rm{\,mH}}</latex>
| |
| - | </primer>
| |
| - |
| |
| - | <primer>
| |
| - | 2. Tuljavi iz prvega primera priključimo v zaporedni vezavi na izmenično napetost 24 V / 1000 Hz. Izračunaj tok skozi tuljavi pri pozitivnem in negativnem medsebojnem magnetnem sklepu k = 0,2.|||
| |
| - | a) pozitivni magnetni sklep
| |
| - |
| |
| - | <latex>L \,=\, {L_1}\, +\, {L_2}\, +\, 2M\, =\, 200\, +\, 300\, +\, 2\, \cdot\, 49\, =\, {\rm{598\,mH}}</latex>
| |
| - |
| |
| - | <latex>{X_L} \,=\, 2\pi fL \,= \,2\pi \, \cdot \,1000 \,\cdot\, {\rm{0,598}}\, =\, 3755\,{\rm{\Omega }}</latex>
| |
| - |
| |
| - | <latex>I\, = \,\frac{U}{X_L} \,=\, \frac{24}{3755}\, =\, {\rm{6,4\,mA}}</latex>
| |
| - |
| |
| - |
| |
| - | b) negativni magnetni sklep
| |
| - |
| |
| - |
| |
| - | <latex>L\, =\, {L_1}\, +\, {L_2}\, -\, 2M\, =\, 200\, +\, 300\, - \,2 \,\cdot\, 49\,= \,{\rm{402\,mH}}</latex>
| |
| - |
| |
| - |
| |
| - | <latex>{X_L} \,=\, 2\pi fL \,=\, 2\pi\, \cdot\, 1000 \,\cdot \,{\rm{0,402}} \,=\, 2492\,{\rm{\Omega }}</latex>
| |
| - |
| |
| - |
| |
| - | <latex>I \,=\, \frac{U}{X_L}\, =\, \frac{24}{2492}\, =\,{\rm{9,6\,mA}}</latex>
| |
| - | </primer>
| |
| - |
| |
| - |
| |
| - |
| |
| - |
| |
| - |
| |
| - | <references />
| |
| | {{Hierarchy footer}} | | {{Hierarchy footer}} |
Tuljave kot elektronske elemente redkeje vežemo zaporedno ali vzporedno. Navitja elektroenergetskih strojev in naprav pa so pogosti primeri različnim vezavam navitij (sl. 5.2.1), transformatorski sklopi tuljav (sl. 5.2.1 c) pa so pogosti tudi na področju elektronike.
V navedenih in podobnih primerih obstaja velika verjetnost, da se magnetni pretok ene tuljave delno sklene tudi skozi ovoje druge tuljave.