Iz e-ELEKTROTEHNIKA plus
(Primerjava redakcij)
m (1 revision) |
|||
| (5 intermediate revisions not shown) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | [[Image: | + | [[Image:eele_slika_visji_004.svg|thumb|Slika 4: Vlak ponavljajočih tokovnih impulzov.]] |
| - | Značilnica periodične funkcije je tudi njena poprečna ali ''srednja vrednost''. Periodo <latex>T</latex> razdelimo na <latex>n</latex> intervalov s trajanji <latex>\Delta t_k</latex>; <latex>k = 1,\,2,\,\,...\,\,n</latex>. V sredini <latex>k</latex>-tega intervala ima napetost določeno vrednost <latex>U_k</latex>. Srednjo vrednost <latex>U_{sr}.</latex> napetosti <latex>u</latex> (označujemo jo tudi s črto nad simbolom) določa izraz | + | Značilnica periodične funkcije je tudi njena poprečna ali ''srednja vrednost''. Periodo <latex>T</latex> razdelimo na <latex>n</latex> intervalov s trajanji <latex>\Delta t_k</latex>; <latex>k = 1,\,2,\,\,...\,\,n</latex>. V sredini <latex>k</latex>-tega intervala ima napetost določeno vrednost <latex>U_k</latex>. Srednjo vrednost <latex>U_{sr}.</latex> napetosti <latex>u</latex> (označujemo jo tudi s črto nad simbolom) določa izraz: |
| Vrstica 6: | Vrstica 6: | ||
| - | Če je periodična funkcija zelo razgibana (spremenljiva), morajo biti intervali <latex>\Delta t_k</latex> ;»kar najkrajši«, v nasprotnem so lahko tudi daljši.<ref>O vsoti sumandov, | + | Če je periodična funkcija zelo razgibana (spremenljiva), morajo biti intervali <latex>\Delta t_k</latex> ;»kar najkrajši«, v nasprotnem so lahko tudi daljši.<ref>O vsoti sumandov, ki jih je veliko in imajo neznatne vrednosti, bomo govorili v zadnjem poglavju, v okviru določenega integrala.</ref> |
| - | '''Zgled 2 | + | '''Zgled 2 ''' |
| - | Multivibrator generira pulzirajočo napetost. V času impulza (<latex>T_1</latex>) ima napetost <latex>u</latex> vrednost <latex>U_0</latex>, v času pavze (<latex>T_2</latex>) pa vrednost 0 V (slika 4).<ref>Multivibrator je posebno elektronsko vezje, ki generira pulzirajočo napetost.</ref> Izrazimo srednjo vrednost napetosti | + | Multivibrator generira pulzirajočo napetost. V času impulza (<latex>T_1</latex>) ima napetost <latex>u</latex> vrednost <latex>U_0</latex>, v času pavze (<latex>T_2</latex>) pa vrednost 0 V (slika 4).<ref>Multivibrator je posebno elektronsko vezje, ki generira pulzirajočo napetost.</ref> Izrazimo srednjo vrednost napetosti. ⇒ Periodo določa vsota dveh časov: <latex>T = T_1 + T_2</latex>. Ker je napetost pulzirajoča, razdelimo periodo <latex>T</latex> na intervala trajanj <latex>T_1</latex> in <latex>T_2</latex>. Po zgornji formuli sledi srednja vrednost napetosti: |
| Vrstica 17: | Vrstica 17: | ||
| - | Primer | + | Primer: V času impulza (trajanja 1 ms) naj ima napetost vrednost 10 V; čas pavze naj bo 3 ms. Iz formule sledi srednja vrednost 2,5 V.<ref>In kako bi komentirali <latex>I_{sr.}</latex>; impulznega toka <latex>i</latex> v primeru instrumenta z vrtljivo tuljavico? Ker okorna tuljavica ne more slediti pogostim impulzom toka, se ustali v legi, ki je sorazmerna <latex>I_{sr.}</latex></ref> Srednjo vrednost periodične funkcije geometrijsko interpretira oddaljenost črte od abscise, ki z obeh strani črte izenačuje površine likov med funkcijo in črto. |
| - | + | ||
| - | |||
| - | + | <references /> | |
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
{{Hierarchy footer}} | {{Hierarchy footer}} | ||
Trenutna redakcija s časom 15:54, 12. julij 2010
Značilnica periodične funkcije je tudi njena poprečna ali srednja vrednost. Periodo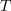

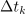
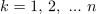
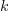
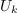
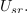

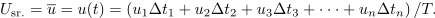
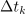
Zgled 2
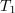

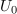
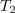
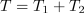
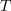
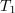
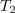
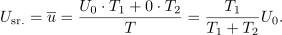
Primer: V času impulza (trajanja 1 ms) naj ima napetost vrednost 10 V; čas pavze naj bo 3 ms. Iz formule sledi srednja vrednost 2,5 V.[3] Srednjo vrednost periodične funkcije geometrijsko interpretira oddaljenost črte od abscise, ki z obeh strani črte izenačuje površine likov med funkcijo in črto.
Opombe
- ↑ O vsoti sumandov, ki jih je veliko in imajo neznatne vrednosti, bomo govorili v zadnjem poglavju, v okviru določenega integrala.
- ↑ Multivibrator je posebno elektronsko vezje, ki generira pulzirajočo napetost.
- ↑ In kako bi komentirali ; impulznega toka
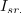 v primeru instrumenta z vrtljivo tuljavico? Ker okorna tuljavica ne more slediti pogostim impulzom toka, se ustali v legi, ki je sorazmerna
v primeru instrumenta z vrtljivo tuljavico? Ker okorna tuljavica ne more slediti pogostim impulzom toka, se ustali v legi, ki je sorazmerna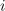
Podpoglavja:
| | 1.1.1.1 Srednja vrednost harmonične funkcije |