e
ELEKTROTEHNIKA
plus
Glavna stran
Kazalo (osnovni nivo)
Kazalo (višji nivo)
Predstavitev projekta
Minimalne zahteve

3.1.3 Izmenični krog z idealiziranim kondenzatorjem

3 Lastnost in zakonitosti izmeničnih krogov
 >> 
3.1 Enostavni, idealizirani izmenični krog
 >> 

Iz e-ELEKTROTEHNIKA plus

(Primerjava redakcij)
Skoči na: navigacija, iskanje
Vrstica 1: Vrstica 1:
-
[[Image:eele_slika_3_1_20.svg|thumb|right|Slika 3.1.20: Odvisnost toka od frekvence v kapacitivnem izmeničnem krogu]]
 
-
[[Image:eele_slika_3_1_21.svg|thumb|right|Slika 3.1.21: Odvisnost kapacitivne upornosti od frekvence in kapacitivnosti]]
 
-
[[Image:eele_slika_3_1_22.svg|thumb|right|Slika 3.1.22: Časovni potek moči v kapacitivnem izmeničnem krogu]]
 
[[Image:eele_slika_3_1_29.svg|thumb|right|Slika 3.1.13]]
[[Image:eele_slika_3_1_29.svg|thumb|right|Slika 3.1.13]]
Vrstica 129: Vrstica 126:
<latex>i\, = \,C \,\cdot\, \frac{\Delta u}{\Delta t}</latex>
<latex>i\, = \,C \,\cdot\, \frac{\Delta u}{\Delta t}</latex>
-
 
+
[[Image:eele_slika_3_1_19.svg|thumb|right|Slika 3.1.19: Hitrost spreminjanja sinusne izmenične napetosti]]
<pomembno>
<pomembno>
-
[[Image:eele_slika_3_1_19.svg|thumb|right|Slika 3.1.19: Hitrost spreminjanja sinusne izmenične napetosti]]
 
*Trenutni tok v izmeničnem krogu s kondenzatorjem je premo sorazmeren s '''kapacitivnostjo''' kondenzatorja in '''hitrostjo spreminjanja napetosti''' na kondenzatorju.</pomembno>
*Trenutni tok v izmeničnem krogu s kondenzatorjem je premo sorazmeren s '''kapacitivnostjo''' kondenzatorja in '''hitrostjo spreminjanja napetosti''' na kondenzatorju.</pomembno>
Vrstica 144: Vrstica 140:
== Odvisnost kapacitivne prevodnosti  ==
== Odvisnost kapacitivne prevodnosti  ==
-
 
+
[[Image:eele_slika_3_1_20.svg|thumb|right|Slika 3.1.20: Odvisnost toka od frekvence v kapacitivnem izmeničnem krogu]]
Odvisnost kapacitivne prevodnosti lahko ugotovimo na podoben način kot pri induktivni upornosti.
Odvisnost kapacitivne prevodnosti lahko ugotovimo na podoben način kot pri induktivni upornosti.
Vrstica 203: Vrstica 199:
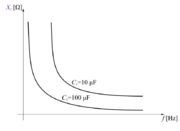
Odvisnost kapacitivne upornosti od frekvence in kapacitivnosti kondenzatorja v grafični obliki prikazuje slika 3.1.21:  
Odvisnost kapacitivne upornosti od frekvence in kapacitivnosti kondenzatorja v grafični obliki prikazuje slika 3.1.21:  
-
 
+
[[Image:eele_slika_3_1_21.svg|thumb|right|Slika 3.1.21: Odvisnost kapacitivne upornosti od frekvence in kapacitivnosti]]
Induktivna in kapacitivna upornost sta si torej v določenih lastnostih '''podobni''' (navidezni, linearni), razlikujeta pa se v povzročanju '''nasprotnih''' faznih kotov in '''obratni frekvenčni odvisnosti'''.  
Induktivna in kapacitivna upornost sta si torej v določenih lastnostih '''podobni''' (navidezni, linearni), razlikujeta pa se v povzročanju '''nasprotnih''' faznih kotov in '''obratni frekvenčni odvisnosti'''.  
Vrstica 242: Vrstica 238:
Iz časovnih potekov napetosti in toka v kapacitivnem izmeničnem krogu (sl. 3.1.18) dobimo na že znani način časovni potek moči (sl. 3.1.22):  
Iz časovnih potekov napetosti in toka v kapacitivnem izmeničnem krogu (sl. 3.1.18) dobimo na že znani način časovni potek moči (sl. 3.1.22):  
-
 
+
[[Image:eele_slika_3_1_22.svg|thumb|right|Slika 3.1.22: Časovni potek moči v kapacitivnem izmeničnem krogu]]
<pomembno>
<pomembno>

Redakcija: 09:45, 11. maj 2010

Slika:Eele slika 3 1 29.svg
Slika 3.1.13

Kondenzator kot element v elektroenergetiki ni tako pogost kot tuljava (navitje), saj je sestavni del le nekaterih elektroenergetskih naprav in električnih omrežij (enofazni elektromotorji, kompenzacija jalove energije …). V elektroniki pa je kondenzator nepogrešljiv element večine naprav (frekvenčne kretnice in filtri, usmerniki, ojačevalniki …), zato je vreden enake pozornosti kot tuljava. Nekaj najpogostejših izvedb kondenzatorjev je na sliki 2.1.15.


Kondenzator v enosmernem in izmeničnem krogu

Slika 3.1.16: Kondenzator v enosmernem in izmeničnem krogu

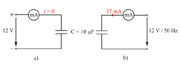
Poskus 3.1.6:

Kondenzator s kapacitivnostjo 10 μF priključimo zaporedno z mA-metrom najprej na enosmerno napetost 12 V (sl. 3.1.16 a) in potem na izmenično sinusno napetost 12 V/50 Hz. Izmerimo toka obeh priključitev in ju primerjajmo med seboj.


  • V primeru enosmerne napetosti je v krogu le kratkotrajni tok polnjenja kondenzatorja[1].
  • V primeru izmenične napetosti je v krogu stalni električni tok.


  • Kondenzator enosmernega toka ne prevaja, izmeničnega pa navidezno prevaja.
  • Za enosmerni tok predstavlja kondenzator neskončno, za izmenični tok končno upornost.


V poskusu 3.1.6 a) smo zaznali le kratkotrajni tok ob sklenitvi električnega kroga. To je bil tok polnjenja kondenzatorja, dielektrik pa je onemogočal tok skozi kondenzator. V poskusu 3.1.6 b) pa izmenična napetost povzroča v električnem krogu tok izmeničnega polnjenja in praznjenja kondenzatorja, čeprav tudi v tem primeru skozi dielektrik kondenzatorja ni toka.


  • Vzrok prevodnosti izmeničnega kroga s kondenzatorjem je izmenično polnjenje in praznjenje kondenzatorja.
  • Prevodnost kondenzatorja v izmeničnem krogu imenujemo kapacitivna prevodnost[2] (BC).


S ponovitvijo poskusa 3.1.6 b) pri stalni kapacitivnosti in frekvenci in različnih napetostih bi ugotovili, da tudi v izmeničnem krogu s kondenzatorjem velja med napetostjo in tokom premo sorazmerje.


  • Kapacitivna prevodnost je pri konstantni kapacitivnosti linearna prevodnost.


Pri zanemarljivi neidealnosti dielektrika kondenzatorja (idealiziranenem kondenzatorju), znani sinusni napetosti na kondenzatorju in znanem toku v električnem krogu s kondenzatorjem lahko kapacitivno prevodnost izračunamo na osnovi razmerja maksimalnih ali efektivnih vrednosti napetosti in toka:



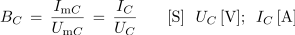
Z obratnim sorazmerjem dobimo kapacitivno upornost[3] kondenzatorja v izmeničnem krogu (XC).



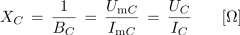
Primer:

Primer:V izmeničnem krogu s kondenzatorjem je tok 12 mA. Kolikšna sta kapacitivna prevodnost in upornost kondenzatorja, če je napetost na kondenzatorju 6 V?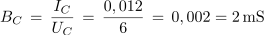
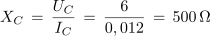
Rešitev




Časovni potek napetosti in toka

Slika 3.1.17: Opazovanje časovnih potekov napetosti in toka v izmeničnem krogu s kondenzatorjem
Slika 3.1.18: Izmenični krog s čisto kapacitivno upornostjo (idealiziranim kondenzatorjem

Poskus 3.1.7:

Kondenzator s kapacitivnostjo C = 1 μF priključimo zaporedno z uporom R = 1 kΩ na izvor sinusne izmenične napetosti 5 V/200 Hz (slika 3.1.17). Na dvokanalnem osciloskopu opazujmo časovni potek padca napetosti na kondenzatorju in toka (padca napetosti na uporu) v krogu s kondenzatorjem.


  • Napetost in tok imata enako, sinusno obliko časovnih potekov.
  • Tok prehiteva napetost za ¼ periode (90 °).


  • Kapacitivnost povzroča v izmeničnem krogu zaostajanje napetosti za tokom.


Kondenzator je v splošnem bližji idealnosti kot tuljava. Kljub temu ga bomo iz enakih razlogov kot pri tuljavi pri nadaljnji obravnavi izmeničnih krogov, če to ne bo potrebno drugače, obravnavali kot idealizirani kondenzator. V takem primeru imamo v izmeničnem krogu samo kapacitivnost (slika 3.1.18 a). Kazalčni in časovni diagram napetosti in toka za kapacitivni izmenični krog sta prikazana na sliki 3.1.18 b) in c).


  • V izmeničnem krogu s čisto kapacitivnostjo napetost zaostaja za tokom za ¼ periode.
  • Fazni kot med tokom in napetostjo v kapacitivnem krogu je - 90 º.



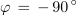
V primerjavi z induktivnim izmeničnim krogom ugotavljamo pomembno dejstvo:


  • Kondenzator povzroči v sinusnem izmeničnem krogu nasprotni fazni premik kot tuljava.


Fazni premik med napetostjo in tokom, ki ga povzroči kapacitivnost v sinusnem izmeničnem krogu, lahko pojasnimo s podobnim razmišljanjem kot pri tuljavi.

Na osnovi enačbe enosmernega toka I = Q ⁄ t [4] lahko zapišemo enačbo za trenutno vrednost izmeničnega toka:



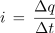
  • Trenutna vrednost izmeničnega toka je podana s trenutnim pretokom elektrine.


Z upoštevanjem enačbe C = Q ⁄ U [5] oziroma Q = C ∙ U dobimo:


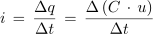
ali

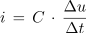
Slika 3.1.19: Hitrost spreminjanja sinusne izmenične napetosti
  • Trenutni tok v izmeničnem krogu s kondenzatorjem je premo sorazmeren s kapacitivnostjo kondenzatorja in hitrostjo spreminjanja napetosti na kondenzatorju.


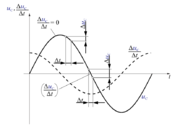
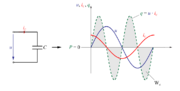
Sinusni izmenični tok v električnem krogu s kondenzatorjem ima torej največjo vrednost v trenutku najhitrejšega spreminjanja napetosti na kondenzatorju in obratno (sl. 3.1.19).


  • Vzrok faznega kota 90 º v izmeničnem krogu s kapacitivno upornostjo je v odvisnosti trenutne vrednosti sinusnega toka od hitrosti spreminjanja napetosti na kondenzatorju.


Odvisnost kapacitivne prevodnosti

Slika 3.1.20: Odvisnost toka od frekvence v kapacitivnem izmeničnem krogu

Odvisnost kapacitivne prevodnosti lahko ugotovimo na podoben način kot pri induktivni upornosti.

Poskus 3.1.8:

Na sinusno izmenično napetost, npr. 6 V/200 Hz, priključimo prek A-metra kondenzator s kapacitivnostjo 1 μF.

a) Spreminjajmo frekvenco od 200 Hz do 1000 Hz in opazujmo jakost toka na A-metru (slika 3.1.20 a).

b) Pri frekvenci 200 Hz zamenjajmo kondenzator s kondenzatorjem 10 μF.


  • Tok pri konstantni kapacitivnosti in napetosti z naraščajočo frekvenco linearno narašča.
  • Tok pri konstantni frekvenci in napetosti z naraščajočo kapacitivnostjo linearno narašča.


Na osnovi dobljene odvisnosti toka lahko sklepamo o frekvenčni odvisnosti kapacitivne prevodnosti:

  • Kapacitivna prevodnost narašča premo sorazmerno s frekvenco in obratno.
  • Kapacitivna prevodnost narašča premo sorazmerno s kapacitivnostjo in obratno.


Razlaga ugotovljene odvisnost temelji na premo sorazmerni odvisnosti toka polnjenja kondenzatorja od kapacivnosti in hitrosti spreminjanja napetosti na kondenzatorju. Ugotovitev



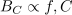
in matematična izpeljava, podobna kot pri tuljavi (<informacije>), vodita v zapis:


<informacije> Enačbo odvisnosti kapacitivne upornosti praviloma izpeljemo z višjo matematiko, informativno pa jo lahko izpeljemo tudi poenostavljeno na podoben način kot pri induktivni upornosti. Namesto z induktivnostjo in hitrostjo spreminjanja toka bomo operirali s kapacitivnostjo in hitrostjo spreminjanja napetosti. </informacije>



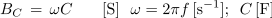
Kapacitivna prevodnost je premo sorazmerna s frekvenco sinusnega toka in kapacitivnostjo kondenzatorja.


Podobno odvisnost kot smo jo pri tuljavi ugotovili za induktivno upornost, ugotavljamo pri kondenzatorju za kapacitivno prevodnost. Kapacitivno upornost XC pa lahko izračunamo z obratno vrednostjo kapacitivne prevodnosti:

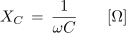
Kapacitivna upornost kondenzatorja je obratno sorazmerna s frekvenco sinusnega izmeničnega toka in kapacitivnostjo kondenzatorja.


Odvisnost kapacitivne upornosti od frekvence in kapacitivnosti kondenzatorja v grafični obliki prikazuje slika 3.1.21:

Slika 3.1.21: Odvisnost kapacitivne upornosti od frekvence in kapacitivnosti

Induktivna in kapacitivna upornost sta si torej v določenih lastnostih podobni (navidezni, linearni), razlikujeta pa se v povzročanju nasprotnih faznih kotov in obratni frekvenčni odvisnosti.

Frekvenčna odvisnost kapacitivne prevodnosti oziroma upornosti je, podobno kot pri tuljavi, osnova za delovanje tonskih kretnic, frekvenčnih filtrov in podobno.


Primeri:

Primer:

1. Izračunaj kapacitivne upornosti kondenzatorja s kapacitivnostjo 10 nF pri frekvencah 50 Hz in 10 MHz.
Rešitev

50 Hz:

100 kHz:

Primer:

2. Kondenzator s kapacitivnostjo 5 μF je priključen na izmenično napetost 110 V/50 Hz. Kolikšen je tok v električnem krogu?
Rešitev



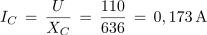
Primer:

3. Kolikšno kapacitivnost mora imeti kondenzator, ki ima pri frekvenci 50 Hz kapacitivno upornost 398 Ω?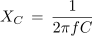
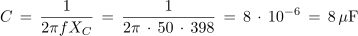
Rešitev




Energija in moč v kapacitivnem izmeničnem krogu (Wel, QC)

V kapacitivnem izmeničnem krogu označujemo trenutno moč s qC, določena pa je s produktom trenutnih vrednosti napetosti in toka:



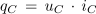
Iz časovnih potekov napetosti in toka v kapacitivnem izmeničnem krogu (sl. 3.1.18) dobimo na že znani način časovni potek moči (sl. 3.1.22):

Slika 3.1.22: Časovni potek moči v kapacitivnem izmeničnem krogu
  • Časovni potek moči sinusnega izmeničnega toka ima v kapacitivnem izmeničnem krogu sinusno obliko z dvojno frekvenco[6] toka.


Pozitivna površina, ki jo v tem primeru oklene krivulja moči s časovno osjo v ¼ periode, predstavlja električno energijo, ki je v omenjeni četrtinki periode pritekla iz generatorja in se nakopičila v električnem polju[7] kondenzatorja.

Zaradi enakosti pozitivne in negativne površine se, podobno kot pri tuljavi, v naslednji četrtinki periode z usihanjem električnega polja v kondenzatorju (slika 3.1.29) nakopičena energija v celoti vrne v generator.


  • Na kondenzatorju se, podobno kot na tuljavi, električna energija ne pretvarja v energijo drugih oblik in se ne sprošča iz električnega kroga.
  • Energija se v kapacitivnem izmeničnem krogu brez učinka (jalovo), z dvojno frekvenco toka, le preliva iz generatorja v kondenzator in obratno. Imenujemo jo jalova energija.


Iz ugotovljenih razlogov imenujemo kapacitivno upornost jalova upornost, tok v kapacitivnem izmeničnem krogu jalovi tok in moč toka v kapacitivnem izmeničnem krogu jalova moč (QC).


  • V primeru faznega kota φ = - 90 ° je v izmeničnem krogu prisotna le jalova moč.


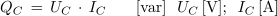
ali tudi


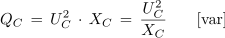
Moč izmeničnega toka v kapacitivnem krogu merimo enako kot v induktivnem krogu v varih.


Opombe

  1. ↑ OE1, str. 188
  2. ↑ Pravimo ji tudi susceptanca.
  3. ↑ Kondenzator se v izmeničnem krogu, podobno kot tuljava, vede re-aktivno – deluje kot breme in generator oziroma ima povratni učinek, zato pravimo upornosti kondenzatorja v izmeničnem krogu tudi reaktanca.
  4. ↑ OE1, str. 35
  5. ↑ OE1, str. 187
  6. ↑
  7. ↑


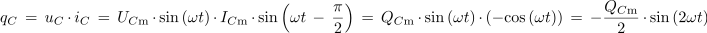
Podpoglavja:


3.1.2.4 Energija in moč v induktivnem izmeničnem krogu 3.1.3.1 Kondenzator v enosmernem in izmeničnem krogu
Vzpostavljeno iz »http://eele.tsckr.si/wiki/index.php/Izmeni%C4%8Dni_krog_z_idealiziranim_kondenzatorjem«

Osebna orodja